HydPy-KinW (base model)¶

The HydPy-KinW model family provides features for implementing storage based routing methods similar to those implemented by the water balance model LARSIM.

Method Features¶

class hydpy.models.kinw.kinw_model.Model[source]¶

Bases: ELSModel, SegmentModel

HydPy-KinW (base model).

The following “inlet update methods” are called in the given sequence at the beginning of each simulation step:

Pick_Q_V1 Query the current inflow from all inlet nodes.
Pick_Inflow_V1 Sum up the current inflow from all inlet nodes.

The following methods define the relevant components of a system of ODE equations (e.g. direct runoff):

Calc_RHM_V1 Regularise the stage with respect to the channel bottom.
Calc_RHMDH_V1 Calculate the derivative of the stage regularised with respect to the channel bottom.
Calc_RHV_V1 Regularise the stage with respect to the transition from the main channel to both forelands.
Calc_RHVDH_V1 Calculate the derivative of the stage regularised with respect to the transition from the main channel to both forelands.
Calc_RHLVR_RHRVR_V1 Regularise the stage with respect to the transitions from the forelands to the outer embankments.
Calc_RHLVRDH_RHRVRDH_V1 Calculate the derivative of the stage regularised with respect to the transition from the forelands to the outer embankments.
Calc_AM_UM_V1 Calculate the wetted area and the wetted perimeter of the main channel.
Calc_AMDH_UMDH_V1 Calculate the derivatives of the wetted area and perimeter of the main channel.
Calc_ALV_ARV_ULV_URV_V1 Calculate the wetted area and wetted perimeter of both forelands.
Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calculate the derivatives of the wetted area and perimeter of both forelands.
Calc_ALVR_ARVR_ULVR_URVR_V1 Calculate the wetted area and perimeter of both outer embankments.
Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calculate the derivatives of the wetted area and perimeter of both outer embankments.
Calc_QM_V1 Calculate the discharge of the main channel after Manning-Strickler.
Calc_QMDH_V1 Calculate the derivative of the discharge of the main channel following method Calc_QM_V1.
Calc_QM_V2 Calculate the discharge of the main channel following the kinematic wave approach.
Calc_QLV_QRV_V1 Calculate the discharge of both forelands after Manning-Strickler.
Calc_QLVDH_QRVDH_V1 Calculate the derivative of both forelands’ discharge with respect to the stage following method Calc_QLV_QRV_V1.
Calc_QLV_QRV_V2 Calculate the discharge of both forelands following the kinematic wave approach.
Calc_QLVR_QRVR_V1 Calculate the discharge of both outer embankments after Manning-Strickler.
Calc_QLVRDH_QRVRDH_V1 Calculate the derivative of the discharge over the outer embankments with respect to the stage following method Calc_QLVR_QRVR_V1.
Calc_QLVR_QRVR_V2 Calculate the discharge of both outer embankments following the kinematic wave approach.
Calc_AG_V1 Calculate the through wetted of the total cross-sections.
Calc_QG_V1 Calculate the discharge of the total cross-section.
Calc_QG_V2 Calculate the discharge of the total cross-section based on an interpolated flow velocity.
Calc_QA_V1 Query the actual outflow.
Calc_WBM_V1 Calculate the water table width above the main channel.
Calc_WBLV_WBRV_V1 Calculate the water table width above both forelands.
Calc_WBLVR_WBRVR_V1 Calculate the water table width above both outer embankments.
Calc_WBG_V1 Calculate the water level width of the total cross-section.
Calc_DH_V1 Determine the change in the stage.

The following methods define the complete equations of an ODE system (e.g. change in storage of fast water due to effective precipitation and direct runoff):

Update_H_V1 Update the stage.
Update_VG_V1 Update the water volume.

The following “outlet update methods” are called in the given sequence at the end of each simulation step:

Pass_Q_V1 Pass the outflow to the outlet node.
Calc_Outflow_V1 Take the inflow as the outflow for channels zero-segment channels.
Pass_Outflow_V1 Pass the outflow to the outlet node.

The following “additional methods” might be called by one or more of the other methods or are meant to be directly called by the user:

Return_QF_V1 Calculate and return the “error” between the actual discharge and the discharge corresponding to the given water stage.
Return_H_V1 Calculate and return the water stage corresponding to the current discharge value.
Update_WaterVolume_V1 Update the old water volume with the current inflow.
Return_InitialWaterVolume_V1 Calculate and return the initial water volume that agrees with the given final water depth following the implicit Euler method.
Return_VolumeError_V1 Calculate and return the difference between the initial water volume that stems from the last simulation step plus the current inflow and the water volume that agrees with the given final water depth following the implicit Euler method.
Calc_WaterDepth_V1 Determine the new water depth based on the implicit Euler method.
Update_WaterVolume_V2 Calculate the new water volume that agrees with the previously calculated final water depth.
Calc_InternalFlow_Outflow_V1 Calculate the flow out of the channel segments.

The following “submodels” might be called by one or more of the implemented methods or are meant to be directly called by the user:

PegasusH Pegasus iterator for finding the correct water stage.
PegasusImplicitEuler Pegasus iterator for determining the water level at the end of a simulation step.

DOCNAME: DocName = ('KinW', 'base model')¶

OBSERVER_METHODS: ClassVar[tuple[type[Method], ...]] = ()¶

wqmodel¶: Required submodel that complies with the following interface: CrossSectionModel_V1.

wqmodel_is_mainmodel¶

wqmodel_typeid¶

REUSABLE_METHODS: ClassVar[tuple[type[ReusableMethod], ...]] = ()¶

class hydpy.models.kinw.kinw_model.Pick_Q_V1[source]¶

Bases: Method

Query the current inflow from all inlet nodes.

Requires the inlet sequence:
Q

Calculates the flux sequence:
QZ

Basic equation:: \(QZ = \sum Q\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> inlets.q.shape = 2
>>> inlets.q = 2.0, 4.0
>>> model.pick_q_v1()
>>> fluxes.qz
qz(6.0)

class hydpy.models.kinw.kinw_model.Pick_Inflow_V1[source]¶

Bases: Method

Sum up the current inflow from all inlet nodes.

Requires the inlet sequence:
Q

Calculates the flux sequence:
Inflow

Basic equation:: \(Inflow = \sum Q\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> inlets.q.shape = 2
>>> inlets.q = 2.0, 4.0
>>> model.pick_inflow_v1()
>>> fluxes.inflow
inflow(6.0)

class hydpy.models.kinw.kinw_model.Calc_QZA_V1[source]¶

Bases: Method

Calculate the current inflow into the channel.

Basic equation:: \(QZA = QZ\)

class hydpy.models.kinw.kinw_model.Calc_RHM_V1[source]¶

Bases: Method

Regularise the stage with respect to the channel bottom.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the derived parameter:
HRP

Requires the state sequence:
H

Calculates the aide sequence:
RHM

Used auxiliary method:: smooth_logistic2()
Basic equation:: \(RHM = smooth_{logistic2}(H, HRP)\)

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> states.h = -1.0, -0.1, 0.0, 0.1, 1.0

>>> hr(0.0)
>>> derived.hrp.update()
>>> model.calc_rhm_v1()
>>> aides.rhm
rhm(0.0, 0.0, 0.0, 0.1, 1.0)

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhm_v1()
>>> aides.rhm
rhm(0.0, 0.01, 0.040983, 0.11, 1.0)

class hydpy.models.kinw.kinw_model.Calc_RHMDH_V1[source]¶

Bases: Method

Calculate the derivative of the stage regularised with respect to the channel bottom.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the derived parameter:
HRP

Requires the state sequence:
H

Calculates the aide sequence:
RHMDH

Used auxiliary method:: smooth_logistic2_derivative2()
Basic equation:: \(RHMDH = smooth_{logistic2'}(H, HRP)\)

Examples:

We apply the class NumericalDifferentiator to validate the calculated derivatives:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> states.h = -1.0, -0.1, 0.0, 0.1, 1.0

>>> hr(0.0)
>>> derived.hrp.update()
>>> model.calc_rhmdh_v1()
>>> aides.rhmdh
rhmdh(0.0, 0.0, 1.0, 1.0, 1.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.rhm],
...     methods=[model.calc_rhm_v1])
>>> numdiff()
d_rhm/d_h: 0.0, 0.0, 1.0, 1.0, 1.0

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhmdh_v1()
>>> aides.rhmdh
rhmdh(0.0, 0.155602, 0.5, 0.844398, 1.0)

>>> numdiff()
d_rhm/d_h: 0.0, 0.155602, 0.5, 0.844398, 1.0

class hydpy.models.kinw.kinw_model.Calc_RHV_V1[source]¶

Bases: Method

Regularise the stage with respect to the transition from the main channel to both forelands.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS HM

Requires the derived parameter:
HRP

Requires the state sequence:
H

Calculates the aide sequence:
RHV

Used auxiliary method:: smooth_logistic2()
Basic equation:: \(RHV = smooth_{logistic2}(H-HM, HRP)\)

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> hm(1.0)
>>> hr(0.1)
>>> derived.hrp.update()
>>> states.h = 0.0, 0.9, 1.0, 1.1, 2.0
>>> model.calc_rhv_v1()
>>> aides.rhv
rhv(0.0, 0.01, 0.040983, 0.11, 1.0)

class hydpy.models.kinw.kinw_model.Calc_RHVDH_V1[source]¶

Bases: Method

Calculate the derivative of the stage regularised with respect to the transition from the main channel to both forelands.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS HM

Requires the derived parameter:
HRP

Requires the state sequence:
H

Calculates the aide sequence:
RHVDH

Used auxiliary method:: smooth_logistic2_derivative2()
Basic equation:: \(RHVDH = smooth_{logistic2'}(H-HM, HRP)\)

Examples:

We apply the class NumericalDifferentiator to validate the calculated derivatives:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> hm(1.0)
>>> states.h = 0.0, 0.9, 1.0, 1.1, 2.0

>>> hr(0.0)
>>> derived.hrp.update()
>>> model.calc_rhvdh_v1()
>>> aides.rhvdh
rhvdh(0.0, 0.0, 1.0, 1.0, 1.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.rhv],
...     methods=[model.calc_rhv_v1])
>>> numdiff()
d_rhv/d_h: 0.0, 0.0, 1.0, 1.0, 1.0

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhvdh_v1()
>>> aides.rhvdh
rhvdh(0.0, 0.155602, 0.5, 0.844398, 1.0)

>>> numdiff()
d_rhv/d_h: 0.0, 0.155602, 0.5, 0.844398, 1.0

class hydpy.models.kinw.kinw_model.Calc_RHLVR_RHRVR_V1[source]¶

Bases: Method

Regularise the stage with respect to the transitions from the forelands to the outer embankments.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS HM

Requires the derived parameters:
HV HRP

Requires the state sequence:
H

Calculates the aide sequences:
RHLVR RHRVR

Used auxiliary method:: smooth_logistic2()
Basic equation:: \(RHVR = smooth_{logistic2}(H-HM-HV, HRP)\)

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(6)
>>> hm(1.0)
>>> hr(0.1)
>>> derived.hv(left=1.0, right=1.1)
>>> derived.hrp.update()
>>> states.h = 1.0, 1.9, 2.0, 2.1, 2.2, 3.0
>>> model.calc_rhlvr_rhrvr_v1()
>>> aides.rhlvr
rhlvr(0.0, 0.01, 0.040983, 0.11, 0.201974, 1.0)
>>> aides.rhrvr
rhrvr(0.0, 0.001974, 0.01, 0.040983, 0.11, 0.9)

class hydpy.models.kinw.kinw_model.Calc_RHLVRDH_RHRVRDH_V1[source]¶

Bases: Method

Calculate the derivative of the stage regularised with respect to the transition from the forelands to the outer embankments.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS HM

Requires the derived parameters:
HRP HV

Requires the state sequence:
H

Calculates the aide sequences:
RHLVRDH RHRVRDH

Used auxiliary method:: smooth_logistic2_derivative2()
Basic equation:: \(RHVDH = smooth_{logistic2'}(H-HM-HV, HRP)\)

Examples:

We apply the class NumericalDifferentiator to validate the calculated derivatives:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(8)
>>> hm(1.0)
>>> derived.hv(left=1.0, right=2.0)
>>> states.h = 1.0, 1.9, 2.0, 2.1, 2.9, 3.0, 3.1, 4.0

>>> hr(0.0)
>>> derived.hrp.update()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> aides.rhlvrdh
rhlvrdh(0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
>>> aides.rhrvrdh
rhrvrdh(0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.rhlvr, aides.rhrvr],
...     methods=[model.calc_rhlvr_rhrvr_v1])
>>> numdiff()
d_rhlvr/d_h: 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
d_rhrvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> aides.rhlvrdh
rhlvrdh(0.0, 0.155602, 0.5, 0.844398, 1.0, 1.0, 1.0, 1.0)
>>> aides.rhrvrdh
rhrvrdh(0.0, 0.0, 0.0, 0.0, 0.155602, 0.5, 0.844398, 1.0)

>>> numdiff()
d_rhlvr/d_h: 0.0, 0.155602, 0.5, 0.844398, 1.0, 1.0, 1.0, 1.0
d_rhrvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.155602, 0.5, 0.844398, 1.0

class hydpy.models.kinw.kinw_model.Calc_AM_UM_V1[source]¶

Bases: Method

Calculate the wetted area and the wetted perimeter of the main channel.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS BM BNM

Requires the derived parameter:
BNMF

Requires the aide sequences:
RHM RHV

Calculates the aide sequences:
AM UM

The main channel is assumed to have identical slopes on both sides. Water flowing exactly above the main channel contributes to AM. Both theoretical surfaces separating the water above the main channel from the water above the forelands contribute to UM.

Examples:

Generally, a trapezoid with reflection symmetry is assumed. Here, we set its smaller base (bottom) to a length of 2 meters, its legs to an inclination of 1 meter per 4 meters, and its height (depths) to 1 meter:
>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(8)
>>> bm(2.0)
>>> bnm(4.0)
>>> derived.bnmf.update()
First, we show that all calculations agree with the unmodified triple trapezoid profile results when setting the smoothing parameter HRP to zero:
>>> derived.hrp(0)
This example deals with normal flow conditions, where water flows within the main channel completely (H < HM, the first five channel sections), and with high flow conditions, where water flows over the foreland also (H > HM, the three last channel sections):
>>> hm(1.0)
>>> states.h = 0.0, 0.1, 0.5, 0.9, 1.0, 1.1, 1.5, 2.0
>>> model.calc_rhm_v1()
>>> model.calc_rhv_v1()
>>> model.calc_am_um_v1()
>>> aides.am
am(0.0, 0.24, 2.0, 5.04, 6.0, 7.0, 11.0, 16.0)
>>> aides.um
um(2.0, 2.824621, 6.123106, 9.42159, 10.246211, 10.446211, 11.246211,
   12.246211)
The next example checks the special case of a channel with zero height:
>>> hm(0.0)
>>> model.calc_rhm_v1()
>>> model.calc_rhv_v1()
>>> model.calc_am_um_v1()
>>> aides.am
am(0.0, 0.2, 1.0, 1.8, 2.0, 2.2, 3.0, 4.0)
>>> aides.um
um(2.0, 2.2, 3.0, 3.8, 4.0, 4.2, 5.0, 6.0)
Second, we repeat both examples with a reasonable smoothing parameterisation. The primary deviations occur around the original discontinuities related to the channel bottom and the main channel’s transition to both forelands:
>>> hr(0.1)
>>> derived.hrp.update()
>>> hm(1.0)
>>> states.h = 0.0, 0.1, 0.5, 0.9, 1.0, 1.1, 1.5, 2.0
>>> model.calc_rhm_v1()
>>> model.calc_rhv_v1()
>>> model.calc_am_um_v1()
>>> aides.am
am(0.088684, 0.2684, 2.000075, 5.0396, 5.993282, 6.9916, 10.99995, 16.0)
>>> aides.um
um(2.337952, 2.907083, 6.123131, 9.359128, 9.990225, 10.383749,
   11.246133, 12.246211)
>>> hm(0.0)
>>> model.calc_rhm_v1()
>>> model.calc_rhv_v1()
>>> model.calc_am_um_v1()
>>> aides.am
am(0.081965, 0.22, 1.000025, 1.8, 2.0, 2.2, 3.0, 4.0)
>>> aides.um
um(2.081965, 2.22, 3.000025, 3.8, 4.0, 4.2, 5.0, 6.0)

class hydpy.models.kinw.kinw_model.Calc_AMDH_UMDH_V1[source]¶

Bases: Method

Calculate the derivatives of the wetted area and perimeter of the main channel.

Requires the control parameters:
GTS BM BNM

Requires the derived parameter:
BNMF

Requires the aide sequences:
RHM RHMDH RHV RHVDH

Calculates the aide sequences:
AMDH UMDH

Examples:

In the following, we repeat the examples of the documentation on method Calc_AM_UM_V1 and check the derivatives’ correctness by comparing the results of class NumericalDifferentiator:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(8)
>>> bm(2.0)
>>> bnm(4.0)

>>> derived.bnmf.update()
>>> derived.hrp(0)

>>> hm(1.0)
>>> states.h = 0.0, 0.1, 0.5, 0.9, 1.0, 1.1, 1.5, 2.0
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_amdh_umdh_v1()
>>> aides.amdh
amdh(2.0, 2.8, 6.0, 9.2, 10.0, 10.0, 10.0, 10.0)
>>> aides.umdh
umdh(8.246211, 8.246211, 8.246211, 8.246211, 2.0, 2.0, 2.0, 2.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.am, aides.um],
...     methods=[model.calc_rhm_v1,
...              model.calc_rhv_v1,
...              model.calc_am_um_v1])
>>> numdiff()
d_am/d_h: 2.0, 2.8, 6.0, 9.2, 10.0, 10.0, 10.0, 10.0
d_um/d_h: 8.246211, 8.246211, 8.246211, 8.246211, 2.0, 2.0, 2.0, 2.0

>>> hm(0.0)
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_amdh_umdh_v1()
>>> aides.amdh
amdh(2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0)
>>> aides.umdh
umdh(2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0)
>>> numdiff()
d_am/d_h: 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0
d_um/d_h: 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0

>>> hr(0.1)
>>> derived.hrp.update()

>>> hm(1.0)
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_amdh_umdh_v1()
>>> aides.amdh
amdh(1.163931, 2.431865, 5.998826, 9.18755, 9.836069, 10.05693,
     10.000749, 10.0)
>>> aides.umdh
umdh(4.123105, 6.963079, 8.243132, 7.274283, 5.123105, 2.971926,
     2.001327, 2.0)

>>> numdiff()
d_am/d_h: 1.163931, 2.431865, 5.998826, 9.18755, 9.836069, 10.05693, 10.000749, 10.0
d_um/d_h: 4.123105, 6.963079, 8.243132, 7.274283, 5.123105, 2.971926, 2.001327, 2.0

class hydpy.models.kinw.kinw_model.Calc_ALV_ARV_ULV_URV_V1[source]¶

Bases: Method

Calculate the wetted area and wetted perimeter of both forelands.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS BV BNV

Requires the derived parameter:
BNVF

Requires the aide sequences:
RHV RHLVR RHRVR

Calculates the aide sequences:
ALV ARV ULV URV

Each foreland lies between the main channel and one outer embankment. The water flowing exactly above a foreland is contributing to ALV or ARV. The theoretical surface separating the water above the main channel from the water above the foreland is not contributing to ULV or URV. On the other hand, the surface separating the water above the foreland from the water above its outer embankment is contributing to ULV and URV.

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(14)
>>> hm(1.0)

First, we show that all calculations agree with the unmodified triple trapezoid profile results when setting the smoothing parameter HRP to zero:

>>> derived.hrp(0)

This example deals with normal flow conditions, where water flows within the main channel completely (H < HM, the first four channel sections); with moderate high flow conditions, where water flows over both forelands, but not over their embankments (HM < H < (HM + HV), channel sections six to eight or twelve for the left and the right foreland, respectively), and with extreme high flow conditions, where water flows over both forelands and their outer embankments ((HM + HV) < H, the last six or two channel sections for the left and the right foreland, respectively):

>>> bv(left=2.0, right=3.0)
>>> bnv(left=4.0, right=5.0)
>>> derived.bnvf.update()
>>> derived.hv(left=1.0, right=2.0)

>>> states.h = (0.0, 0.5, 0.9, 1.0, 1.1, 1.5, 1.9,
...             2.0, 2.1, 2.5, 2.9, 3.0, 3.1, 4.0)
>>> model.calc_rhm_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alv_arv_ulv_urv_v1()
>>> aides.alv
alv(0.0, 0.0, 0.0, 0.0, 0.22, 1.5, 3.42, 4.0, 4.6, 7.0, 9.4, 10.0, 10.6,
    16.0)
>>> aides.arv
arv(0.0, 0.0, 0.0, 0.0, 0.325, 2.125, 4.725, 5.5, 6.325, 10.125, 14.725,
    16.0, 17.3, 29.0)
>>> aides.ulv
ulv(2.0, 2.0, 2.0, 2.0, 2.412311, 4.061553, 5.710795, 6.123106,
    6.223106, 6.623106, 7.023106, 7.123106, 7.223106, 8.123106)
>>> aides.urv
urv(3.0, 3.0, 3.0, 3.0, 3.509902, 5.54951, 7.589118, 8.09902, 8.608921,
    10.648529, 12.688137, 13.198039, 13.298039, 14.198039)

The next example proves the correct handling of forelands with zero widths and heights:

>>> bv(left=0.0, right=2.0)
>>> bnv(4.0)
>>> derived.hv(left=1.0, right=0.0)
>>> model.calc_rhv_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alv_arv_ulv_urv_v1()
>>> aides.alv
alv(0.0, 0.0, 0.0, 0.0, 0.02, 0.5, 1.62, 2.0, 2.4, 4.0, 5.6, 6.0, 6.4,
    10.0)
>>> aides.arv
arv(0.0, 0.0, 0.0, 0.0, 0.2, 1.0, 1.8, 2.0, 2.2, 3.0, 3.8, 4.0, 4.2, 6.0)
>>> aides.ulv
ulv(0.0, 0.0, 0.0, 0.0, 0.412311, 2.061553, 3.710795, 4.123106,
    4.223106, 4.623106, 5.023106, 5.123106, 5.223106, 6.123106)
>>> aides.urv
urv(2.0, 2.0, 2.0, 2.0, 2.1, 2.5, 2.9, 3.0, 3.1, 3.5, 3.9, 4.0, 4.1, 5.0)

Second, we repeat both examples with a reasonable smoothing parameterisation. The primary deviations occur around the original discontinuities related to the channel bottom and the main channel’s transition to both forelands:

>>> hr(0.1)
>>> derived.hrp.update()

>>> bv(left=2.0, right=3.0)
>>> bnv(left=4.0, right=5.0)
>>> derived.hv(left=1.0, right=2.0)
>>> model.calc_rhv_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alv_arv_ulv_urv_v1()
>>> aides.alv
alv(0.0, 0.000025, 0.0202, 0.085324, 0.2442, 1.50005, 3.4198, 3.996641,
    4.5958, 6.999975, 9.4, 10.0, 10.6, 16.0)
>>> aides.arv
arv(0.0, 0.000038, 0.03025, 0.127147, 0.36025, 2.125069, 4.725, 5.5,
    6.325, 10.125, 14.72475, 15.995801, 17.29475, 29.0)
>>> aides.ulv
ulv(2.0, 2.000052, 2.041231, 2.168976, 2.453542, 4.061565, 5.679564,
    5.995113, 6.191875, 6.623066, 7.023106, 7.123106, 7.223106, 8.123106)
>>> aides.urv
urv(3.0, 3.000064, 3.05099, 3.208971, 3.560892, 5.549574, 7.589118,
    8.09902, 8.608921, 10.648478, 12.647147, 13.03005, 13.257049,
    14.198039)

>>> bv(left=0.0, right=2.0)
>>> bnv(4.0)
>>> derived.hv(left=1.0, right=0.0)
>>> model.calc_rhm_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alv_arv_ulv_urv_v1()
>>> aides.alv
alv(0.0, 0.0, 0.0002, 0.003359, 0.0242, 0.500025, 1.6198, 1.996641,
    2.3958, 3.999975, 5.6, 6.0, 6.4, 10.0)
>>> aides.arv
arv(0.0, 0.000025, 0.02, 0.081965, 0.22, 1.000025, 1.8, 2.0, 2.2, 3.0,
    3.8, 4.0, 4.2, 6.0)
>>> aides.ulv
ulv(0.0, 0.000052, 0.041231, 0.168976, 0.453542, 2.061565, 3.679564,
    3.995113, 4.191875, 4.623066, 5.023106, 5.123106, 5.223106, 6.123106)
>>> aides.urv
urv(2.0, 2.000013, 2.01, 2.040983, 2.11, 2.500013, 2.9, 3.0, 3.1, 3.5,
    3.9, 4.0, 4.1, 5.0)

class hydpy.models.kinw.kinw_model.Calc_ALVDH_ARVDH_ULVDH_URVDH_V1[source]¶

Bases: Method

Calculate the derivatives of the wetted area and perimeter of both forelands.

Requires the control parameters:
GTS BV BNV

Requires the derived parameter:
BNVF

Requires the aide sequences:
RHV RHVDH RHLVR RHLVRDH RHRVR RHRVRDH

Calculates the aide sequences:
ALVDH ARVDH ULVDH URVDH

Examples:

In the following, we repeat the examples of the documentation on method Calc_ALV_ARV_ULV_URV_V1 and check the derivatives’ correctness by comparing the results of class NumericalDifferentiator:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(13)
>>> hm(1.0)
>>> bv(left=2.0, right=3.0)
>>> bnv(left=4.0, right=5.0)
>>> derived.bnvf.update()
>>> derived.hv(left=1.0, right=2.0)

>>> derived.hrp(0)

>>> states.h = (1.0, 1.5, 1.9, 2.0, 2.1, 2.5, 3.0,
...             3.5, 3.9, 4.0, 4.1, 4.5, 5.0)
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvdh_arvdh_ulvdh_urvdh_v1()
>>> aides.alvdh
alvdh(2.0, 4.0, 5.6, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0)
>>> aides.arvdh
arvdh(3.0, 5.5, 7.5, 8.0, 8.5, 10.5, 13.0, 13.0, 13.0, 13.0, 13.0, 13.0,
      13.0)
>>> aides.ulvdh
ulvdh(4.123106, 4.123106, 4.123106, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
      1.0, 1.0, 1.0)
>>> aides.urvdh
urvdh(5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 1.0, 1.0,
      1.0, 1.0, 1.0, 1.0, 1.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.alv, aides.arv, aides.ulv, aides.urv],
...     methods=[model.calc_rhv_v1,
...              model.calc_rhlvr_rhrvr_v1,
...              model.calc_alv_arv_ulv_urv_v1])
>>> numdiff()
d_alv/d_h: 2.0, 4.0, 5.6, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0
d_arv/d_h: 3.0, 5.5, 7.5, 8.0, 8.5, 10.5, 13.0, 13.0, 13.0, 13.0, 13.0, 13.0, 13.0
d_ulv/d_h: 4.123106, 4.123106, 4.123106, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
d_urv/d_h: 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0

>>> bv(left=0.0, right=2.0)
>>> bnv(4.0)
>>> derived.bnvf.update()
>>> derived.hv(left=1.0, right=0.0)
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvdh_arvdh_ulvdh_urvdh_v1()
>>> aides.alvdh
alvdh(0.0, 2.0, 3.6, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0)
>>> aides.arvdh
arvdh(2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0)
>>> aides.ulvdh
ulvdh(4.123106, 4.123106, 4.123106, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
      1.0, 1.0, 1.0)
>>> aides.urvdh
urvdh(1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
>>> numdiff()
d_alv/d_h: 0.0, 2.0, 3.6, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0
d_arv/d_h: 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0
d_ulv/d_h: 4.123106, 4.123106, 4.123106, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
d_urv/d_h: 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0

>>> hr(0.1)
>>> derived.hrp.update()

>>> bv(left=2.0, right=3.0)
>>> bnv(left=4.0, right=5.0)
>>> derived.bnvf.update()
>>> derived.hv(left=1.0, right=2.0)

>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvdh_arvdh_ulvdh_urvdh_v1()
>>> aides.alvdh
alvdh(1.081965, 3.9992, 5.593775, 5.918034, 6.028465, 6.000375, 6.0,
      6.0, 6.0, 6.0, 6.0, 6.0, 6.0)
>>> aides.arvdh
arvdh(1.602457, 5.498894, 7.499998, 8.0, 8.5, 10.5, 12.897543,
      13.000468, 13.000001, 13.0, 13.0, 13.0, 13.0)
>>> aides.ulvdh
ulvdh(2.061553, 4.121566, 3.637142, 2.561553, 1.485963, 1.000664, 1.0,
      1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
>>> aides.urvdh
urvdh(2.54951, 5.097936, 5.099018, 5.099019, 5.099018, 5.098149,
      3.04951, 1.000871, 1.000001, 1.0, 1.0, 1.0, 1.0)

>>> numdiff()
d_alv/d_h: 1.081965, 3.9992, 5.593775, 5.918034, 6.028465, 6.000375, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0, 6.0
d_arv/d_h: 1.602457, 5.498894, 7.499998, 8.0, 8.5, 10.5, 12.897543, 13.000468, 13.000001, 13.0, 13.0, 13.0, 13.0
d_ulv/d_h: 2.061553, 4.121566, 3.637142, 2.561553, 1.485963, 1.000664, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
d_urv/d_h: 2.54951, 5.097936, 5.099018, 5.099019, 5.099018, 5.098149, 3.04951, 1.000871, 1.000001, 1.0, 1.0, 1.0, 1.0

class hydpy.models.kinw.kinw_model.Calc_ALVR_ARVR_ULVR_URVR_V1[source]¶

Bases: Method

Calculate the wetted area and perimeter of both outer embankments.

Required by the method:
Return_QF_V1

Requires the control parameters:
GTS BNVR

Requires the derived parameter:
BNVRF

Requires the aide sequences:
RHLVR RHRVR

Calculates the aide sequences:
ALVR ARVR ULVR URVR

Each outer embankment lies beyond its foreland. The water flowing exactly above an embankment adds to ALVR and ARVR. The theoretical surface separating water above the foreland from the water above its embankment is not contributing to ULVR and URVR.

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(11)
>>> hm(1.0)

First, we show that all calculations agree with the unmodified triple trapezoid profile results when the setting the smoothing parameter HRP to zero:

>>> derived.hrp(0)

This example deals with moderate high flow conditions, where water flows over the forelands, but not over their outer embankments (HM < H < (HM + HV), the first four or eight channel sections for the left and the right outer embankment, respectively); the second example deals with extreme high flow conditions, where water flows both over the foreland and their outer embankments ((HM + HV) < H, the last seven or three channel sections for the left and the right outer embankment, respectively):

>>> states.h = 1.0, 1.5, 1.9, 2.0, 2.1, 2.5, 2.9, 3.0, 3.1, 3.5, 4.0
>>> bnvr(left=4.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alvr_arvr_ulvr_urvr_v1()
>>> aides.alvr
alvr(0.0, 0.0, 0.0, 0.0, 0.02, 0.5, 1.62, 2.0, 2.42, 4.5, 8.0)
>>> aides.arvr
arvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.025, 0.625, 2.5)
>>> aides.ulvr
ulvr(0.0, 0.0, 0.0, 0.0, 0.412311, 2.061553, 3.710795, 4.123106,
     4.535416, 6.184658, 8.246211)
>>> aides.urvr
urvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.509902, 2.54951, 5.09902)

The next example checks the special cases of a vertical outer embankment (left side) and zero-height foreland (right side):

>>> bnvr(left=0.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=0.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alvr_arvr_ulvr_urvr_v1()
>>> aides.alvr
alvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
>>> aides.arvr
arvr(0.0, 0.625, 2.025, 2.5, 3.025, 5.625, 9.025, 10.0, 11.025, 15.625,
     22.5)
>>> aides.ulvr
ulvr(0.0, 0.0, 0.0, 0.0, 0.1, 0.5, 0.9, 1.0, 1.1, 1.5, 2.0)
>>> aides.urvr
urvr(0.0, 2.54951, 4.589118, 5.09902, 5.608921, 7.648529, 9.688137,
     10.198039, 10.707941, 12.747549, 15.297059)

Second, we repeat both examples with a reasonable smoothing parameterisation. The primary deviations occur around the original discontinuities related to the channel bottom and the main channel’s transition to both forelands:

>>> hr(0.1)
>>> derived.hrp.update()
>>> bnvr(left=4.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alvr_arvr_ulvr_urvr_v1()
>>> aides.alvr
alvr(0.0, 0.0, 0.0002, 0.003359, 0.0242, 0.500025, 1.62, 2.0, 2.42, 4.5,
     8.0)
>>> aides.arvr
arvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.00025, 0.004199, 0.03025, 0.625031,
     2.5)
>>> aides.ulvr
ulvr(0.0, 0.000052, 0.041231, 0.168976, 0.453542, 2.061605, 3.710795,
     4.123106, 4.535416, 6.184658, 8.246211)
>>> aides.urvr
urvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.000064, 0.05099, 0.208971, 0.560892,
     2.549574, 5.09902)

>>> bnvr(left=0.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=0.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_alvr_arvr_ulvr_urvr_v1()
>>> aides.alvr
alvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
>>> aides.arvr
arvr(0.004199, 0.625031, 2.025, 2.5, 3.025, 5.625, 9.025, 10.0, 11.025,
     15.625, 22.5)
>>> aides.ulvr
ulvr(0.0, 0.000013, 0.01, 0.040983, 0.11, 0.500013, 0.9, 1.0, 1.1, 1.5,
     2.0)
>>> aides.urvr
urvr(0.208971, 2.549574, 4.589118, 5.09902, 5.608921, 7.648529,
     9.688137, 10.198039, 10.707941, 12.747549, 15.297059)

class hydpy.models.kinw.kinw_model.Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1[source]¶

Bases: Method

Calculate the derivatives of the wetted area and perimeter of both outer embankments.

Requires the control parameters:
GTS BNVR

Requires the derived parameter:
BNVRF

Requires the aide sequences:
RHLVR RHLVRDH RHRVR RHRVRDH

Calculates the aide sequences:
ALVRDH ARVRDH ULVRDH URVRDH

Examples:

In the following, we repeat the examples of the documentation on method Calc_ALVR_ARVR_ULVR_URVR_V1 and check the derivatives’ correctness by comparing the results of class NumericalDifferentiator:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(11)
>>> hm(1.0)

>>> derived.hrp(0)

>>> states.h = 1.0, 1.5, 1.9, 2.0, 2.1, 2.5, 2.9, 3.0, 3.1, 3.5, 4.0
>>> bnvr(left=4.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvrdh_arvrdh_ulvrdh_urvrdh_v1()
>>> aides.alvrdh
alvrdh(0.0, 0.0, 0.0, 0.0, 0.4, 2.0, 3.6, 4.0, 4.4, 6.0, 8.0)
>>> aides.arvrdh
arvrdh(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.5, 2.5, 5.0)
>>> aides.ulvrdh
ulvrdh(0.0, 0.0, 0.0, 4.123106, 4.123106, 4.123106, 4.123106, 4.123106,
       4.123106, 4.123106, 4.123106)
>>> aides.urvrdh
urvrdh(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 5.09902, 5.09902, 5.09902,
       5.09902)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.alvr, aides.arvr, aides.ulvr, aides.urvr],
...     methods=[model.calc_rhlvr_rhrvr_v1,
...              model.calc_alvr_arvr_ulvr_urvr_v1])
>>> numdiff()
d_alvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.4, 2.0, 3.6, 4.0, 4.4, 6.0, 8.0
d_arvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.5, 2.5, 5.0
d_ulvr/d_h: 0.0, 0.0, 0.0, 4.123106, 4.123106, 4.123106, 4.123106, 4.123106, 4.123106, 4.123106, 4.123106
d_urvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 5.09902, 5.09902, 5.09902, 5.09902

>>> bnvr(left=0.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=0.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvrdh_arvrdh_ulvrdh_urvrdh_v1()
>>> aides.alvrdh
alvrdh(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
>>> aides.arvrdh
arvrdh(0.0, 2.5, 4.5, 5.0, 5.5, 7.5, 9.5, 10.0, 10.5, 12.5, 15.0)
>>> aides.ulvrdh
ulvrdh(0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0)
>>> aides.urvrdh
urvrdh(5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902,
       5.09902, 5.09902, 5.09902, 5.09902)

>>> numdiff()
d_alvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0
d_arvr/d_h: 0.0, 2.5, 4.5, 5.0, 5.5, 7.5, 9.5, 10.0, 10.5, 12.5, 15.0
d_ulvr/d_h: 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0
d_urvr/d_h: 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902, 5.09902

>>> hr(0.1)
>>> derived.hrp.update()
>>> bnvr(left=4.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvrdh_arvrdh_ulvrdh_urvrdh_v1()
>>> aides.alvrdh
alvrdh(0.0, 0.0, 0.006224, 0.081965, 0.371535, 1.999625, 3.599999, 4.0,
       4.4, 6.0, 8.0)
>>> aides.arvrdh
arvrdh(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.00778, 0.102457, 0.464419,
       2.499532, 5.0)
>>> aides.ulvrdh
ulvrdh(0.0, 0.000876, 0.641565, 2.061553, 3.48154, 4.12223, 4.123105,
       4.123105, 4.123106, 4.123106, 4.123106)
>>> aides.urvrdh
urvrdh(0.0, 0.0, 0.0, 0.0, 0.000001, 0.001083, 0.79342, 2.54951,
       4.305599, 5.097936, 5.099019)

>>> numdiff()
d_alvr/d_h: 0.0, 0.0, 0.006224, 0.081965, 0.371535, 1.999625, 3.599999, 4.0, 4.4, 6.0, 8.0
d_arvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.00778, 0.102457, 0.464419, 2.499532, 5.0
d_ulvr/d_h: 0.0, 0.000876, 0.641565, 2.061553, 3.48154, 4.12223, 4.123105, 4.123105, 4.123106, 4.123106, 4.123106
d_urvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.000001, 0.001083, 0.79342, 2.54951, 4.305599, 5.097936, 5.099019

class hydpy.models.kinw.kinw_model.Calc_QM_V1[source]¶

Bases: Method

Calculate the discharge of the main channel after Manning-Strickler.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the derived parameter:
MFM

Requires the aide sequences:
AM UM

Calculates the aide sequence:
QM

Basic equation:: \(QM = MFM \cdot \frac{AM^{5/3}}{UM^{2/3}}\)

Examples:

Note the handling of zero values for UM (in the third subsection):

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(3)
>>> derived.mfm(10.0)
>>> aides.am = 3.0, 0.0, 3.0
>>> aides.um = 7.0, 7.0, 0.0
>>> model.calc_qm_v1()
>>> aides.qm
qm(17.053102, 0.0, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QM_V2[source]¶

Bases: Method

Calculate the discharge of the main channel following the kinematic wave approach.

Requires the control parameter:
GTS

Requires the aide sequences:
AM QMDH AMDH

Calculates the aide sequence:
QM

Basic equation:: \(QM = \frac{QMDH}{AMDH} \cdot AM\)

Examples:

Note the handling of zero values for AMDH (in the second subsection):

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> aides.am = 4.0, 4.0
>>> aides.qmdh = 3.0, 3.0
>>> aides.amdh = 2.0, 0.0
>>> model.calc_qm_v2()
>>> aides.qm
qm(6.0, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QMDH_V1[source]¶

Bases: Method

Calculate the derivative of the discharge of the main channel following method Calc_QM_V1.

Requires the control parameter:
GTS

Requires the derived parameter:
MFM

Requires the aide sequences:
AM AMDH UM UMDH

Calculates the aide sequence:
QMDH

Basic equation:: \(QMDH = MFM \cdot \frac{5 \cdot AM^{2/3} \cdot AMDH}{3 \cdot UM^{2/3}} - \frac{2 \cdot AM^{5/3} \cdot UMDH}{3 \cdot UM^{5/3}}\)

Examples:

First, we apply the class NumericalDifferentiator to validate the calculated derivatives:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> bm(2.0)
>>> bnm(4.0)
>>> hm(2.0)
>>> derived.mfm(10.0)
>>> derived.hrp(0.0)
>>> derived.bnmf.update()
>>> states.h = 0.0, 1.0
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_am_um_v1()
>>> model.calc_amdh_umdh_v1()
>>> model.calc_qmdh_v1()
>>> aides.qmdh
qmdh(0.0, 94.12356)

>>> from hydpy import NumericalDifferentiator,pub
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.qm],
...     methods=[model.calc_rhm_v1,
...              model.calc_rhv_v1,
...              model.calc_am_um_v1,
...              model.calc_qm_v1],
...     dx=1e-8)
>>> with pub.options.reprdigits(5):
...     numdiff()
d_qm/d_h: 0.00002, 94.12356

Second, we show that zero values for AM or UM result in zero values for QMDH:

>>> aides.am = 1.0, 0.0
>>> aides.um = 0.0, 1.0
>>> model.calc_qmdh_v1()
>>> aides.qmdh
qmdh(0.0, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QLV_QRV_V1[source]¶

Bases: Method

Calculate the discharge of both forelands after Manning-Strickler.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the derived parameter:
MFV

Requires the aide sequences:
ALV ARV ULV URV

Calculates the aide sequences:
QLV QRV

Basic equation:: \(QV = MFV \cdot \frac{AV^{5/3}}{UV^{2/3}}\)

Examples:

Note the handling of zero values for ULV and URV (in the second subsection):

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> derived.mfv(left=10.0, right=18.0)
>>> aides.alv = 3.0, 3.0
>>> aides.arv = 4.0, 4.0
>>> aides.ulv = 7.0, 0.0
>>> aides.urv = 8.0, 0.0
>>> model.calc_qlv_qrv_v1()
>>> aides.qlv
qlv(17.053102, 0.0)
>>> aides.qrv
qrv(45.357158, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QLV_QRV_V2[source]¶

Bases: Method

Calculate the discharge of both forelands following the kinematic wave approach.

Requires the control parameter:
GTS

Requires the aide sequences:
ALV ARV ALVDH ARVDH QLVDH QRVDH

Calculates the aide sequences:
QLV QRV

Basic equation:: \(QV = \frac{QVDH}{AVDH} \cdot AV\)

Examples:

Note the handling of zero values for ALVDH and ARVDH (in the second subsection):

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> aides.alv = 3.0, 3.0
>>> aides.arv = 5.0, 5.0
>>> aides.qlvdh = 4.0, 4.0
>>> aides.qrvdh = 6.0, 6.0
>>> aides.alvdh = 2.0, 0.0
>>> aides.arvdh = 4.0, 0.0
>>> model.calc_qlv_qrv_v2()
>>> aides.qlv
qlv(6.0, 0.0)
>>> aides.qrv
qrv(7.5, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QLVDH_QRVDH_V1[source]¶

Bases: Method

Calculate the derivative of both forelands’ discharge with respect to the stage following method Calc_QLV_QRV_V1.

Requires the control parameter:
GTS

Requires the derived parameter:
MFV

Requires the aide sequences:
ALV ALVDH ARV ARVDH ULV ULVDH URV URVDH

Calculates the aide sequences:
QLVDH QRVDH

Basic equation:: \(QVDH = MFV \cdot \frac{5 \cdot AV^{2/3} \cdot AVDH}{3 \cdot UV^{2/3}} - \frac{2 \cdot AV^{5/3} \cdot UVDH}{3 \cdot UV^{5/3}}\)

Examples:

First, we apply the class NumericalDifferentiator to validate the calculated derivatives:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> hm(1.0)
>>> bv(left=2.0, right=3.0)
>>> bnv(left=4.0, right=5.0)
>>> derived.bnvf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> derived.mfv(left=10.0, right=18.0)
>>> derived.hrp(0.0)
>>> states.h = 0.5, 1.5
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alv_arv_ulv_urv_v1()
>>> model.calc_alvdh_arvdh_ulvdh_urvdh_v1()
>>> model.calc_qlvdh_qrvdh_v1()
>>> aides.qlvdh
qlvdh(0.0, 29.091363)
>>> aides.qrvdh
qrvdh(0.0, 74.651886)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.qlv, aides.qrv],
...     methods=[model.calc_rhv_v1,
...              model.calc_rhlvr_rhrvr_v1,
...              model.calc_alv_arv_ulv_urv_v1,
...              model.calc_qlv_qrv_v1])()
d_qlv/d_h: 0.0, 29.091363
d_qrv/d_h: 0.0, 74.651886

Second, we show that zero values for ALV or ULV as well as for ARV or URV result in zero values for QLVDH or QRVDH, respectively:

>>> aides.alv = 1.0, 0.0
>>> aides.ulv = 0.0, 1.0
>>> aides.arv = 1.0, 0.0
>>> aides.urv = 0.0, 1.0
>>> model.calc_qlvdh_qrvdh_v1()
>>> aides.qlvdh
qlvdh(0.0, 0.0)
>>> aides.qrvdh
qrvdh(0.0, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QLVR_QRVR_V1[source]¶

Bases: Method

Calculate the discharge of both outer embankments after Manning-Strickler.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the derived parameter:
MFV

Requires the aide sequences:
ALVR ARVR ULVR URVR

Calculates the aide sequences:
QLVR QRVR

Basic equation:: \(QVR = MFV \cdot \frac{AVR^{5/3}}{UVR^{2/3}}\)

Examples:

Note the handling of zero values for ULVR and URVR (in the second subsection):

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> derived.mfv(left=10.0, right=1.2)
>>> aides.alvr = 3.0, 3.0
>>> aides.arvr = 4.0, 4.0
>>> aides.ulvr = 7.0, 0.0
>>> aides.urvr = 8.0, 0.0
>>> model.calc_qlvr_qrvr_v1()
>>> aides.qlvr
qlvr(17.053102, 0.0)
>>> aides.qrvr
qrvr(3.023811, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QLVR_QRVR_V2[source]¶

Bases: Method

Calculate the discharge of both outer embankments following the kinematic wave approach.

Requires the control parameter:
GTS

Requires the aide sequences:
ALVR ARVR QLVRDH QRVRDH ALVRDH ARVRDH

Calculates the aide sequences:
QLVR QRVR

Basic equation:: \(QVR = \frac{QVRDH}{AVRDH} \cdot AVR\)

Examples:

Note the handling of zero values for ALVRDH and ARVRDH (in the second subsection):

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> aides.alvr = 3.0, 3.0
>>> aides.arvr = 5.0, 5.0
>>> aides.qlvrdh = 4.0, 4.0
>>> aides.qrvrdh = 6.0, 6.0
>>> aides.alvrdh = 2.0, 0.0
>>> aides.arvrdh = 4.0, 0.0
>>> model.calc_qlvr_qrvr_v2()
>>> aides.qlvr
qlvr(6.0, 0.0)
>>> aides.qrvr
qrvr(7.5, 0.0)

class hydpy.models.kinw.kinw_model.Calc_QLVRDH_QRVRDH_V1[source]¶

Bases: Method

Calculate the derivative of the discharge over the outer embankments with respect to the stage following method Calc_QLVR_QRVR_V1.

Requires the control parameter:
GTS

Requires the derived parameter:
MFV

Requires the aide sequences:
ALVR ALVRDH ARVR ARVRDH ULVR ULVRDH URVR URVRDH

Calculates the aide sequences:
QLVRDH QRVRDH

Basic equation:: \(QVRDH = MFVR \cdot \frac{5 \cdot AVR^{2/3} \cdot AVRDH}{3 \cdot UVR^{2/3}} - \frac{2 \cdot AVR{5/3} \cdot UVRDH}{3 \cdot UVR^{5/3}}\)

Examples:

First, we apply the class NumericalDifferentiator to validate the calculated derivatives:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> hm(1.0)
>>> bnvr(left=4.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> derived.mfv(left=10.0, right=18.0)
>>> derived.hrp(0.0)
>>> states.h = 1.5, 3.5
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_alvr_arvr_ulvr_urvr_v1()
>>> model.calc_alvrdh_arvrdh_ulvrdh_urvrdh_v1()
>>> model.calc_qlvrdh_qrvrdh_v1()
>>> aides.qlvrdh
qlvrdh(0.0, 64.717418)
>>> aides.qrvrdh
qrvrdh(0.0, 23.501747)

>>> from hydpy import NumericalDifferentiator
>>> NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.qlvr, aides.qrvr],
...     methods=[model.calc_rhlvr_rhrvr_v1,
...              model.calc_alvr_arvr_ulvr_urvr_v1,
...              model.calc_qlvr_qrvr_v1])()
d_qlvr/d_h: 0.0, 64.717418
d_qrvr/d_h: 0.0, 23.501747

Second, we show that zero values for ALVR or ULVR as well as for ARVR or URVR result in zero values for QLVRDH or QRVRDH, respectively:

>>> aides.alvr = 1.0, 0.0
>>> aides.ulvr = 0.0, 1.0
>>> aides.arvr = 1.0, 0.0
>>> aides.urvr = 0.0, 1.0
>>> model.calc_qlvrdh_qrvrdh_v1()
>>> aides.qlvrdh
qlvrdh(0.0, 0.0)
>>> aides.qrvrdh
qrvrdh(0.0, 0.0)

class hydpy.models.kinw.kinw_model.Calc_AG_V1[source]¶

Bases: Method

Calculate the through wetted of the total cross-sections.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the aide sequences:
AM ALV ARV ALVR ARVR

Calculates the aide sequence:
AG

Basic equation:: \(AG = AM+ALV+ARV+ALVR+ARVR\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> aides.am = 0.0, 1.0
>>> aides.alv = 2.0, 4.0
>>> aides.arv = 3.0, 5.0
>>> aides.alvr = 6.0, 8.0
>>> aides.arvr = 7.0, 9.0
>>> model.calc_ag_v1()
>>> aides.ag
ag(18.0, 27.0)

class hydpy.models.kinw.kinw_model.Calc_QG_V1[source]¶

Bases: Method

Calculate the discharge of the total cross-section.

Required by the method:
Return_QF_V1

Requires the control parameter:
GTS

Requires the aide sequences:
QM QLV QRV QLVR QRVR

Calculates the flux sequence:
QG

Basic equation:: \(QG = QM + QLV + QRV + QLVR + QRVR\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> aides.qm = 0.0, 1.0
>>> aides.qlv = 2.0, 4.0
>>> aides.qrv = 3.0, 5.0
>>> aides.qlvr = 6.0, 8.0
>>> aides.qrvr = 7.0, 9.0
>>> model.calc_qg_v1()
>>> fluxes.qg
qg(18.0, 27.0)

class hydpy.models.kinw.kinw_model.Calc_QG_V2[source]¶

Bases: Method

Calculate the discharge of the total cross-section based on an interpolated flow velocity.

Requires the control parameters:
GTS Laen VG2FG EK

Requires the state sequence:
VG

Calculates the flux sequence:
QG

Basic equation:: \(QG = EK \cdot \frac{1000 \cdot V_{interpolated} \cdot VG \cdot GTS}{Laen}\)

Example:

For simplicity, we define a linear between flow velocity and water storage:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> laen(10.0)
>>> ek(0.5)
>>> vg2fg(PPoly.from_data(xs=[0.0, 1.0], ys=[0.0, 1.0]))
>>> from hydpy import UnitTest
>>> test = UnitTest(model,
...                 model.calc_qg_v2,
...                 last_example=3,
...                 parseqs=(states.vg,
...                          fluxes.qg))
>>> test.nexts.vg = numpy.empty((4, 2))
>>> test.nexts.vg[:, 0] = numpy.arange(-1.0, 3.0)
>>> test.nexts.vg[:, 1] = numpy.arange(3.0, 7.0)
>>> test()
| ex. |        vg |            qg |
-----------------------------------
|   1 | -1.0  3.0 |   0.0   900.0 |
|   2 |  0.0  4.0 |   0.0  1600.0 |
|   3 |  1.0  5.0 | 100.0  2500.0 |

Our example shows that a linear velocity-volume relationship results in a quadratic discharge-volume relationship. Note also that we generally set the discharge to zero for negative volumes.

For more realistic approximations of measured relationships between storage and discharge, we require larger neural networks.

class hydpy.models.kinw.kinw_model.Calc_WBM_V1[source]¶

Bases: Method

Calculate the water table width above the main channel.

Requires the control parameters:
GTS BM BNM

Requires the fixed parameters:
WBMin WBReg

Requires the aide sequences:
RHM RHMDH RHV RHVDH

Calculates the aide sequence:
WBM

Examples:

Due to \(WBM = \frac{dAM}{dh}\), we can apply the class NumericalDifferentiator to validate the calculated water table widths:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> bm(4.0)
>>> bnm(2.0)
>>> hm(1.0)
>>> hr(0.0)
>>> derived.hrp.update()
>>> states.h = 0.0, 0.9, 1.0, 1.1, 2.0
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_wbm_v1()
>>> aides.wbm
wbm(4.0, 7.6, 8.0, 8.0, 8.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.am],
...     methods=[model.calc_rhm_v1,
...              model.calc_rhv_v1,
...              model.calc_am_um_v1])
>>> numdiff()
d_am/d_h: 4.0, 7.6, 8.0, 8.0, 8.0

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_wbm_v1()
>>> aides.wbm
wbm(2.081965, 7.593774, 7.918034, 8.028465, 8.0)

>>> numdiff()
d_am/d_h: 2.081965, 7.593774, 7.918034, 8.028465, 8.0

class hydpy.models.kinw.kinw_model.Calc_WBLV_WBRV_V1[source]¶

Bases: Method

Calculate the water table width above both forelands.

Requires the control parameters:
GTS BV BNV

Requires the aide sequences:
RHV RHVDH RHLVR RHLVRDH RHRVR RHRVRDH

Calculates the aide sequences:
WBLV WBRV

Examples:

Due to \(WBV = \frac{dAV}{dh}\), we can apply the class NumericalDifferentiator to validate the calculated water table widths:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(11)
>>> bm(4.0)
>>> bnm(2.0)
>>> derived.bnvf.update()
>>> hm(1.0)
>>> bv(left=2.0, right=3.0)
>>> bbv(left=10., right=40.)
>>> bnv(left=10., right=20.)
>>> derived.hv.update()
>>> derived.hv
hv(left=1.0, right=2.0)
>>> hr(0.0)
>>> derived.hrp.update()
>>> states.h = 1.0, 1.5, 1.9, 2.0, 2.1, 2.5, 2.9, 3.0, 3.1, 3.5, 4.0
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_wblv_wbrv_v1()
>>> aides.wblv
wblv(2.0, 7.0, 11.0, 12.0, 12.0, 12.0, 12.0, 12.0, 12.0, 12.0, 12.0)
>>> aides.wbrv
wbrv(3.0, 13.0, 21.0, 23.0, 25.0, 33.0, 41.0, 43.0, 43.0, 43.0, 43.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.alv, aides.arv],
...     methods=[model.calc_rhv_v1,
...              model.calc_rhlvr_rhrvr_v1,
...              model.calc_alv_arv_ulv_urv_v1])
>>> numdiff()
d_alv/d_h: 2.0, 7.0, 11.0, 12.0, 12.0, 12.0, 12.0, 12.0, 12.0, 12.0, 12.0
d_arv/d_h: 3.0, 13.0, 21.0, 23.0, 25.0, 33.0, 41.0, 43.0, 43.0, 43.0, 43.0

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_wblv_wbrv_v1()
>>> aides.wblv
wblv(1.204913, 6.998638, 10.984437, 11.795086, 12.071163, 12.000937,
     12.000002, 12.0, 12.0, 12.0, 12.0)
>>> aides.wbrv
wbrv(1.909826, 12.997489, 20.999995, 22.999999, 25.0, 33.0, 40.96888,
     42.590174, 43.142325, 43.001873, 43.000001)

>>> numdiff()
d_alv/d_h: 1.204913, 6.998638, 10.984437, 11.795086, 12.071163, 12.000937, 12.000002, 12.0, 12.0, 12.0, 12.0
d_arv/d_h: 1.909826, 12.997489, 20.999995, 22.999999, 25.0, 33.0, 40.96888, 42.590174, 43.142325, 43.001873, 43.000001

class hydpy.models.kinw.kinw_model.Calc_WBLVR_WBRVR_V1[source]¶

Bases: Method

Calculate the water table width above both outer embankments.

Requires the control parameters:
GTS BNVR

Requires the aide sequences:
RHLVR RHLVRDH RHRVR RHRVRDH

Calculates the aide sequences:
WBLVR WBRVR

Examples:

Due to \(WBVR = \frac{dAVR}{dh}\), we can apply the class NumericalDifferentiator to validate the calculated water table widths:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(11)
>>> hm(1.0)
>>> bnvr(left=4.0, right=5.0)
>>> derived.bnvrf.update()
>>> derived.hv(left=1.0, right=2.0)
>>> hr(0.0)
>>> derived.hrp.update()
>>> states.h = 1.0, 1.5, 1.9, 2.0, 2.1, 2.5, 2.9, 3.0, 3.1, 3.5, 4.0
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_wblvr_wbrvr_v1()
>>> aides.wblvr
wblvr(0.0, 0.0, 0.0, 0.0, 0.4, 2.0, 3.6, 4.0, 4.4, 6.0, 8.0)
>>> aides.wbrvr
wbrvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.5, 2.5, 5.0)

>>> from hydpy import NumericalDifferentiator
>>> numdiff = NumericalDifferentiator(
...     xsequence=states.h,
...     ysequences=[aides.alvr, aides.arvr],
...     methods=[model.calc_rhlvr_rhrvr_v1,
...              model.calc_alvr_arvr_ulvr_urvr_v1])
>>> numdiff()
d_alvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.4, 2.0, 3.6, 4.0, 4.4, 6.0, 8.0
d_arvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.5, 2.5, 5.0

>>> hr(0.1)
>>> derived.hrp.update()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_wblvr_wbrvr_v1()
>>> aides.wblvr
wblvr(0.0, 0.0, 0.006224, 0.081965, 0.371535, 1.999625, 3.599999, 4.0,
      4.4, 6.0, 8.0)
>>> aides.wbrvr
wbrvr(0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.00778, 0.102457, 0.464419,
      2.499532, 5.0)

>>> numdiff()
d_alvr/d_h: 0.0, 0.0, 0.006224, 0.081965, 0.371535, 1.999625, 3.599999, 4.0, 4.4, 6.0, 8.0
d_arvr/d_h: 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.00778, 0.102457, 0.464419, 2.499532, 5.0

class hydpy.models.kinw.kinw_model.Calc_WBG_V1[source]¶

Bases: Method

Calculate the water level width of the total cross-section.

Requires the control parameter:
GTS

Requires the aide sequences:
WBM WBLV WBRV WBLVR WBRVR

Calculates the aide sequence:
WBG

Basic equation:: \(WBG = WBM+WLV+WRV+WLVR+WRVR\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(2)
>>> aides.wbm = 0.0, 1.0
>>> aides.wblv = 2.0, 4.0
>>> aides.wbrv = 3.0, 5.0
>>> aides.wblvr = 6.0, 8.0
>>> aides.wbrvr = 7.0, 9.0
>>> model.calc_wbg_v1()
>>> aides.wbg
wbg(18.0, 27.0)

class hydpy.models.kinw.kinw_model.Calc_DH_V1[source]¶

Bases: Method

Determine the change in the stage.

Requires the control parameters:
Laen GTS

Requires the flux sequences:
QZ QG

Requires the aide sequence:
WBG

Calculates the flux sequence:
DH

Basic equation:: \(DH = \frac{QG_{i-1}-QG_i}{WBG \cdot 1000 \cdot Laen / GTS}\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> laen(10.0)
>>> gts(5)
>>> aides.wbg(3.0, 3.5, 4.0, 3.5, 3.0)
>>> fluxes.qz = 1.0
>>> fluxes.qg = 2.0, 3.0, 4.0, 3.0, 2.0
>>> model.calc_dh_v1()
>>> fluxes.dh
dh(-0.000167, -0.000143, -0.000125, 0.000143, 0.000167)

class hydpy.models.kinw.kinw_model.Update_H_V1[source]¶

Bases: Method

Update the stage.

Requires the control parameter:
GTS

Requires the derived parameter:
Sek

Requires the flux sequence:
DH

Updates the state sequence:
H

Basic equation:: \(\frac{dH}{dt} = DH\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> derived.sek(60*60)
>>> fluxes.dh = -0.12, -0.1, -0.09, 0.1, 0.12
>>> fluxes.dh /= 60*60
>>> states.h(1.0, 1.2, 1.3, 1.2, 1.0)
>>> model.update_h_v1()
>>> states.h
h(0.88, 1.1, 1.21, 1.3, 1.12)

class hydpy.models.kinw.kinw_model.Update_VG_V1[source]¶

Bases: Method

Update the water volume.

Requires the control parameter:
GTS

Requires the derived parameter:
Sek

Requires the flux sequences:
QZA QG

Updates the state sequence:
VG

Basic equation:: \(\frac{dV}{dt} = QG_{i-1}-QG_i\)

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(5)
>>> derived.sek(60*60)
>>> states.vg(1.0, 1.2, 1.3, 1.2, 1.0)
>>> fluxes.qza = 1.0
>>> fluxes.qg = 3.0, 2.0, 4.0, 3.0, 5.0
>>> model.update_vg_v1()
>>> states.vg
vg(0.9928, 1.2036, 1.2928, 1.2036, 0.9928)

class hydpy.models.kinw.kinw_model.Calc_QA_V1[source]¶

Bases: Method

Query the actual outflow.

Requires the control parameter:
GTS

Requires the flux sequences:
QZ QG

Calculates the flux sequence:
QA

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(3)
>>> fluxes.qz = 1.0
>>> fluxes.qg = 2.0, 3.0, 4.0
>>> model.calc_qa_v1()
>>> fluxes.qa
qa(4.0)
>>> gts(0)
>>> model.calc_qa_v1()
>>> fluxes.qa
qa(1.0)

class hydpy.models.kinw.kinw_model.Update_WaterVolume_V1[source]¶

Bases: Method

Update the old water volume with the current inflow.

Requires the derived parameter:
Seconds

Requires the flux sequences:
Inflow InternalFlow

Updates the state sequence:
WaterVolume

Examples:

Method Update_WaterVolume_V1 uses the value of sequence Inflow for the first segment and the respective values of sequences InternalFlow for the remaining segments:

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> nmbsegments(3)
>>> derived.seconds(1e6)
>>> states.watervolume.old = 2.0, 3.0, 4.0
>>> fluxes.inflow = 1.0
>>> fluxes.internalflow = 2.0, 3.0
>>> model.run_segments(model.update_watervolume_v1)
>>> from hydpy import print_vector
>>> print_vector(states.watervolume.old)
3.0, 5.0, 7.0

Negative inflow values are acceptable, even if they result in negative amounts of stored water:

>>> fluxes.inflow = -4.0
>>> fluxes.internalflow = -6.0, -6.0
>>> model.run_segments(model.update_watervolume_v1)
>>> print_vector(states.watervolume.old)
-1.0, -1.0, 1.0

class hydpy.models.kinw.kinw_model.Return_InitialWaterVolume_V1[source]¶

Bases: Method

Calculate and return the initial water volume that agrees with the given final water depth following the implicit Euler method.

Required by the method:
Return_VolumeError_V1

Requires the control parameters:
Length NmbSegments

Requires the derived parameter:
Seconds

Basic equation:: \[\begin{split}A \cdot l / n \cdot 10^{-3} + Q \cdot s \cdot 10^{-6} \\ \\ d = waterdepth \\ A = f_{get\_wettedarea}(d) \\ l = Length \\ n = NmbSegments \\ Q = f_{get\_discharge}(d) \\ s = Seconds\end{split}\]

Examples:

The calculated initial volume is the sum of the water volume at the end of the simulation step and the outflow during the simulation step:
>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> length(100.0)
>>> nmbsegments(10)
>>> derived.seconds(60 * 60 * 24)
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(1)
...     bottomlevels(1.0)
...     bottomwidths(20.0)
...     sideslopes(0.0)
...     bottomslope(0.001)
...     stricklercoefficients(30.0)
...     calibrationfactors(1.0)
>>> from hydpy import round_
>>> round_(model.return_initialwatervolume_v1(2.0))
5.008867
If a segment has zero length, it can, of course, store no water. Hence, the returned value then only comprises the volume of the outflow of the current simulation step:
>>> length(0.0)
>>> round_(model.return_initialwatervolume_v1(2.0))
4.608867
Method Return_InitialWaterVolume_V1 handles cases where the number of segments is zero as if the channel’s length is zero (even if it is inconsistently set to a larger value):
>>> length(100.0)
>>> nmbsegments(0)
>>> round_(model.return_initialwatervolume_v1(2.0))
4.608867

class hydpy.models.kinw.kinw_model.Return_VolumeError_V1[source]¶

Bases: Method

Calculate and return the difference between the initial water volume that stems from the last simulation step plus the current inflow and the water volume that agrees with the given final water depth following the implicit Euler method.

Required by the method:
Calc_WaterDepth_V1

Required submethod:
Return_InitialWaterVolume_V1

Requires the control parameters:
Length NmbSegments

Requires the derived parameter:
Seconds

Requires the state sequence:
WaterVolume

Basic equation:: \[\begin{split}V_1 - V_2 \\ \\ V_1 = WaterVolume \\ V_2 = f_{Return\_InitialWaterVolume\_V1}(waterdepth)\end{split}\]

Examples:

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> length(100.0)
>>> nmbsegments(10)
>>> derived.seconds(60 * 60 * 24)
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(1)
...     bottomlevels(1.0)
...     bottomwidths(20.0)
...     sideslopes(0.0)
...     bottomslope(0.001)
...     stricklercoefficients(30.0)
...     calibrationfactors(1.0)
>>> states.watervolume(4.0)
>>> from hydpy import round_
>>> round_(model.return_volumeerror_v1(2.0))
-1.008867

For a given water depth of zero, Return_VolumeError_V1 simply returns the old value of WaterVolume to safe computation efforts:

>>> round_(model.return_volumeerror_v1(0.0))
4.0

The following example shows that this simplification is correct:

>>> round_(model.return_volumeerror_v1(1e-6))
4.0

class hydpy.models.kinw.kinw_model.PegasusImplicitEuler(model: Model)[source]¶

Bases: Pegasus

Pegasus iterator for determining the water level at the end of a simulation step.

METHODS: ClassVar[tuple[type[Method], ...]] = (<class 'hydpy.models.kinw.kinw_model.Return_VolumeError_V1'>,)¶

name: ClassVar[str] = 'pegasusimpliciteuler'¶

class hydpy.models.kinw.kinw_model.Calc_WaterDepth_V1[source]¶

Bases: Method

Determine the new water depth based on the implicit Euler method.

Required submethod:
Return_VolumeError_V1

Requires the control parameters:
Length NmbSegments

Requires the derived parameters:
Seconds NmbDiscontinuities FinalDepth2InitialVolume

Requires the solver parameters:
WaterVolumeTolerance WaterDepthTolerance

Requires the state sequence:
WaterVolume

Calculates the factor sequence:
WaterDepth

Examples:

Compared to other (explicit) routing methods, the iterative approach of method Calc_WaterDepth_V1 to determine the final water depth for each river segment iteratively leads to high efficiency and (theoretically) absolute stability for short channel segments (namely, stiff problems with a high Courant number). However, be aware that the accuracy of this iteration affects the overall simulation. We begin demonstrating this with a single trapezoid and default numerical values:
>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> length(100.0)
>>> nmbsegments(1)
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(1)
...     bottomlevels(1.0)
...     bottomwidths(20.0)
...     sideslopes(0.0)
...     bottomslope(0.001)
...     stricklercoefficients(30.0)
...     calibrationfactors(1.0)
>>> derived.seconds(60 * 60 * 24)
>>> derived.nmbdiscontinuities.update()
>>> derived.finaldepth2initialvolume.update()
>>> solver.watervolumetolerance.update()
>>> solver.waterdepthtolerance.update()
>>> model.idx_segment = 0
The following test function prints the resulting water depth for several initial volumes and also prints the water volume-related error tolerance (internally calculated as \(WaterVolumeTolerance \cdot InitialWaterVolume\)) and the actual error:
>>> from hydpy import print_vector
>>> def check_search_algorithm():
...     print("volume", "depth", "tolerance", "error")
...     for target_volume in (0.0, 0.1, 1.0, 2.0, 5.0, 10.0, 100.0):
...         states.watervolume.old = target_volume
...         model.calc_waterdepth_v1()
...         depth = factors.waterdepth.values[0]
...         volume = model.return_initialwatervolume_v1(depth)
...         tolerance = solver.watervolumetolerance * target_volume
...         error = target_volume - volume
...         print_vector([target_volume, depth, tolerance, error])
All required and achieved accuracies are below the printed precisions:
>>> check_search_algorithm()
volume depth tolerance error
0.0, 0.0, 0.0, 0.0
0.1, 0.045296, 0.0, 0.0
1.0, 0.356485, 0.0, 0.0
2.0, 0.632911, 0.0, 0.0
5.0, 1.312357, 0.0, 0.0
10.0, 2.244486, 0.0, 0.0
100.0, 13.729876, 0.0, 0.0
If one wishes to improve accuracy or speed up the computation, it is preferable to decrease or increase WaterVolumeTolerance. Here, we increase it and observe that higher numerical errors result:
>>> solver.watervolumetolerance(1e-4)
>>> check_search_algorithm()
volume depth tolerance error
0.0, 0.0, 0.0, 0.0
0.1, 0.045296, 0.00001, 0.0
1.0, 0.356498, 0.0001, -0.000042
2.0, 0.632912, 0.0002, -0.000004
5.0, 1.312356, 0.0005, 0.000004
10.0, 2.244563, 0.001, -0.000447
100.0, 13.729886, 0.01, -0.000091
Alternatively, one can modify the solver parameter WaterDepthTolerance, whose value is used without any modification:
>>> solver.watervolumetolerance(0.0)
>>> solver.waterdepthtolerance(1e-2)
>>> check_search_algorithm()
volume depth tolerance error
0.0, 0.0, 0.0, 0.0
0.1, 0.045296, 0.0, 0.0
1.0, 0.356498, 0.0, -0.000042
2.0, 0.632912, 0.0, -0.000004
5.0, 1.312356, 0.0, 0.000004
10.0, 2.244563, 0.0, -0.000447
100.0, 13.729876, 0.0, 0.0
Now, we define a profile geometry consisting of 3 stacked trapezes:
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(3)
...     bottomlevels(1.0, 3.0, 5.0)
...     bottomwidths(20.0)
...     sideslopes(0.0, 0.0, 0.0)
...     bottomslope(0.001)
...     stricklercoefficients(30.0)
...     calibrationfactors(1.0)
>>> derived.nmbdiscontinuities.update()
>>> derived.finaldepth2initialvolume.update()
>>> solver.watervolumetolerance.update()
>>> solver.waterdepthtolerance.update()
Method Calc_WaterDepth_V1 uses the relevant bottom depths of these trapezes as boundaries for the Pegasus method so that the corresponding discontinuities cannot slow down its convergence:
>>> check_search_algorithm()
volume depth tolerance error
0.0, 0.0, 0.0, 0.0
0.1, 0.045296, 0.0, 0.0
1.0, 0.356503, 0.0, -0.000059
2.0, 0.632918, 0.0, -0.000027
5.0, 1.312357, 0.0, 0.0
10.0, 2.170538, 0.0, 0.0
100.0, 7.624652, 0.0, -0.000004
In the last example, the default tolerance values result in practically likely irrelevant but still recognisable inaccuracies. The following example shows that decreasing the water depth-related tolerance reduces these errors:
>>> solver.waterdepthtolerance(1e-8)
>>> check_search_algorithm()
volume depth tolerance error
0.0, 0.0, 0.0, 0.0
0.1, 0.045296, 0.0, 0.0
1.0, 0.356485, 0.0, 0.0
2.0, 0.632911, 0.0, 0.0
5.0, 1.312357, 0.0, 0.0
10.0, 2.170538, 0.0, 0.0
100.0, 7.624652, 0.0, 0.0

class hydpy.models.kinw.kinw_model.Update_WaterVolume_V2[source]¶

Bases: Method

Calculate the new water volume that agrees with the previously calculated final water depth.

Requires the control parameters:
Length NmbSegments

Requires the factor sequence:
WaterDepth

Updates the state sequence:
WaterVolume

Basic equation:: \[\begin{split}V = A \cdot l / n \cdot 10^{-3} \\ \\ V = WaterVolume \\ A = f_{get\_wettedarea}(D) \\ l = Length \\ n = NmbSegments\end{split}\]

Examples:

Note that, usually, the W-Q submodel must have been processed with the correct final water depth beforehand so that it can provide the related wetted area:

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> length(100.0)
>>> nmbsegments(1)
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(1)
...     bottomlevels(1.0)
...     sideslopes(0.0)
...     calibrationfactors(1.0)
>>> model.wqmodel.sequences.factors.wettedarea = 2.0
>>> model.idx_segment = 0
>>> model.update_watervolume_v2()
>>> states.watervolume
watervolume(0.2)

For zero water depths or channel lengths, Update_WaterVolume_V2 sets the final water volume to zero (independent of the submodel’s currentl wetted area):

>>> model.wqmodel.sequences.factors.wettedarea = -999.0
>>> factors.waterdepth = 0.0
>>> model.update_watervolume_v2()
>>> states.watervolume
watervolume(0.0)
>>> factors.waterdepth = 1.0
>>> length(0.0)
>>> model.update_watervolume_v2()
>>> states.watervolume
watervolume(0.0)

class hydpy.models.kinw.kinw_model.Calc_InternalFlow_Outflow_V1[source]¶

Bases: Method

Calculate the flow out of the channel segments.

Requires the control parameter:
NmbSegments

Requires the derived parameter:
Seconds

Requires the state sequence:
WaterVolume

Calculates the flux sequences:
InternalFlow Outflow

Basic equation:: \[\begin{split}IO = (V_{old} - V_{new}) / s \cdot 1e6 \\ \\ IO = InternalFlow \ or Outflow \\ V = WaterVolume \\ s = Seconds\end{split}\]

Example:

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> nmbsegments(3)
>>> derived.seconds(1e6)
>>> states.watervolume.old = 5.0, 2.0, 4.0
>>> states.watervolume.new = 1.0, 4.0, 2.0
>>> model.run_segments(model.calc_internalflow_outflow_v1)
>>> fluxes.outflow
outflow(2.0)
>>> fluxes.internalflow
internalflow(4.0, -2.0)

class hydpy.models.kinw.kinw_model.Calc_Outflow_V1[source]¶

Bases: Method

Take the inflow as the outflow for channels zero-segment channels.

Requires the control parameter:
NmbSegments

Requires the flux sequence:
Inflow

Calculates the flux sequence:
Outflow

Basic equation:: \[Outflow = Inflow\]

Examples:

Method Calc_Outflow_V1 serves as a stopgap to ensure that the inflow is correctly passed to the outflow if a model does not contain any segments:

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> fluxes.inflow = 1.0
>>> fluxes.outflow = 0.0

>>> nmbsegments(1)
>>> model.calc_outflow_v1()
>>> fluxes.outflow
outflow(0.0)

>>> nmbsegments(0)
>>> model.calc_outflow_v1()
>>> fluxes.outflow
outflow(1.0)

class hydpy.models.kinw.kinw_model.Pass_Q_V1[source]¶

Bases: Method

Pass the outflow to the outlet node.

Requires the flux sequence:
QA

Calculates the outlet sequence:
Q

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> fluxes.qa = 2.0
>>> model.pass_q_v1()
>>> outlets.q
q(2.0)

class hydpy.models.kinw.kinw_model.Pass_Outflow_V1[source]¶

Bases: Method

Pass the outflow to the outlet node.

Requires the flux sequence:
Outflow

Calculates the outlet sequence:
Q

Example:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> fluxes.outflow = 2.0
>>> model.pass_outflow_v1()
>>> outlets.q
q(2.0)

class hydpy.models.kinw.kinw_model.Return_QF_V1[source]¶

Bases: Method

Calculate and return the “error” between the actual discharge and the discharge corresponding to the given water stage.

Required by the method:
Return_H_V1

Required submethods:
Calc_RHM_V1 Calc_RHMDH_V1 Calc_RHV_V1 Calc_RHVDH_V1 Calc_RHLVR_RHRVR_V1 Calc_RHLVRDH_RHRVRDH_V1 Calc_AM_UM_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_ALVR_ARVR_ULVR_URVR_V1 Calc_QM_V1 Calc_QLV_QRV_V1 Calc_QLVR_QRVR_V1 Calc_AG_V1 Calc_QG_V1

Requires the control parameters:
GTS HM BM BNM BV BNV BNVR

Requires the derived parameters:
HV HRP BNMF BNVF BNVRF MFM MFV

Calculates the state sequence:
H

Calculates the aide sequences:
RHM RHMDH RHV RHVDH RHLVR RHRVR RHLVRDH RHRVRDH AM UM ALV ARV ULV URV ALVR ARVR ULVR URVR QM QLV QRV QLVR QRVR AG

Basic equation:: \(Q(H) - QG_0\)

Method Return_QF_V1 is a helper function not intended for performing simulation runs but for easing the implementation of method calculate_characteristiclength() of application model kinw_williams (and similar functionalities). More specifically, it defines the target function for the iterative root search triggered by method Return_H_V1.

While method Return_QF_V1 performs discharge calculations for all stream subsections, it evaluates only those of the first subsection. Accordingly, to avoid wasting computation time, one should not initialise more than one subsection before calling method Return_QF_V1 (or methods Return_H_V1 or calculate_characteristiclength()).

Example:

We reuse the example given in the main documentation on module kinw_williams:
>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> simulationstep("30m")
>>> gts(1)
>>> laen(100.0)
>>> gef(0.00025)
>>> bm(15.0)
>>> bnm(5.0)
>>> skm(1.0/0.035)
>>> hm(6.0)
>>> bv(100.0)
>>> bbv(20.0)
>>> bnv(10.0)
>>> bnvr(100.0)
>>> skv(10.0)
>>> ekm(1.0)
>>> ekv(1.0)
>>> hr(0.1)
>>> parameters.update()
A water stage of 1 m results in a discharge of 7.7 m³/s:
>>> states.h = 1.0
>>> model.calc_rhm_v1()
>>> model.calc_rhmdh_v1()
>>> model.calc_rhv_v1()
>>> model.calc_rhvdh_v1()
>>> model.calc_rhlvr_rhrvr_v1()
>>> model.calc_rhlvrdh_rhrvrdh_v1()
>>> model.calc_am_um_v1()
>>> model.calc_alv_arv_ulv_urv_v1()
>>> model.calc_alvr_arvr_ulvr_urvr_v1()
>>> model.calc_qm_v1()
>>> model.calc_qlv_qrv_v1()
>>> model.calc_qlvr_qrvr_v1()
>>> model.calc_ag_v1()
>>> model.calc_qg_v1()
>>> fluxes.qg
qg(7.745345)
The calculated QG value serves as the “true” value. Now, when passing stage values of 0.5 and 1.0 m, method Return_QF_V1 calculates the corresponding discharge values and returns the “errors” -5.5 m³/s (a stage of 0.5 m results in a too-small discharge value) and 0.0 m³/s (1.0 m is the “true” stage), respectively:
>>> from hydpy import round_
>>> round_(model.return_qf_v1(0.5))
-5.474691
>>> round_(model.return_qf_v1(1.0))
0.0
Note that method Return_QF_V1 does not overwrite the first entry of QG, which would complicate its application within an iterative approach.

Technical checks:

Note that method Return_QF_V1 calculates the value of sequence QG temporarily and resets it afterwards, and calculates all other values of the mentioned sequences without resetting:

>>> from hydpy.core.testtools import check_selectedvariables
>>> from hydpy.models.kinw.kinw_model import Return_QF_V1
>>> print(check_selectedvariables(Return_QF_V1))
Definitely missing: qg
Possibly missing (REQUIREDSEQUENCES):
    Calc_RHM_V1: H
    Calc_RHMDH_V1: H
    Calc_RHV_V1: H
    Calc_RHVDH_V1: H
    Calc_RHLVR_RHRVR_V1: H
    Calc_RHLVRDH_RHRVRDH_V1: H
    Calc_AM_UM_V1: RHM and RHV
    Calc_ALV_ARV_ULV_URV_V1: RHV, RHLVR, and RHRVR
    Calc_ALVR_ARVR_ULVR_URVR_V1: RHLVR and RHRVR
    Calc_QM_V1: AM and UM
    Calc_QLV_QRV_V1: ALV, ARV, ULV, and URV
    Calc_QLVR_QRVR_V1: ALVR, ARVR, ULVR, and URVR
    Calc_AG_V1: AM, ALV, ARV, ALVR, and ARVR
    Calc_QG_V1: QM, QLV, QRV, QLVR, and QRVR
Possibly missing (RESULTSEQUENCES):
    Calc_QG_V1: QG

class hydpy.models.kinw.kinw_model.Return_H_V1[source]¶

Bases: Method

Calculate and return the water stage corresponding to the current discharge value.

Required submethod:
Return_QF_V1

Requires the control parameters:
GTS HM BM BNM BV BNV BNVR

Requires the derived parameters:
HV HRP BNMF BNVF BNVRF MFM MFV

Calculates the state sequence:
H

Calculates the aide sequences:
RHM RHMDH RHV RHVDH RHLVR RHRVR RHLVRDH RHRVRDH AM UM ALV ARV ULV URV ALVR ARVR ULVR URVR QM QLV QRV QLVR QRVR AG

Method Return_H_V1 is a helper function not for performing simulation runs but for easing the implementation of method calculate_characteristiclength() of application model kinw_williams (or similar functionalities). It performs a root search by applying the Pegasus method implemented in module rootutils on the target method Return_QF_V1. Hence, please see the additional application notes in the documentation on method Return_QF_V1.

Example:

We recreate the exact parameterisation as in the example of the documentation on method Return_QF_V1:

>>> from hydpy.models.kinw import *
>>> simulationstep("30m")
>>> parameterstep()

>>> gts(1)
>>> laen(100.0)
>>> gef(0.00025)
>>> bm(15.0)
>>> bnm(5.0)
>>> skm(1.0/0.035)
>>> hm(6.0)
>>> bv(100.0)
>>> bbv(20.0)
>>> bnv(10.0)
>>> bnvr(100.0)
>>> skv(10.0)
>>> ekm(1.0)
>>> ekv(1.0)
>>> hr(0.1)
>>> parameters.update()

For a given discharge value of 7.7 m³/s (discussed in the documentation on method Return_QF_V1), method Return_H_V1 correctly determines the water stage of 1 m:

>>> fluxes.qg = 7.745345
>>> from hydpy import print_vector, round_
>>> round_(model.return_h_v1())
1.0

To evaluate our implementation’s reliability, we search for water stages covering an extensive range of discharge values. The last printed column shows that method Return_H_V1 finds the correct water stage in all cases:

>>> import numpy
>>> for q in [0.0]+list(numpy.logspace(-6, 6, 13)):
...     fluxes.qg = q
...     h = model.return_h_v1()
...     states.h = h
...     model.calc_rhm_v1()
...     model.calc_rhmdh_v1()
...     model.calc_rhv_v1()
...     model.calc_rhvdh_v1()
...     model.calc_rhlvr_rhrvr_v1()
...     model.calc_rhlvrdh_rhrvrdh_v1()
...     model.calc_am_um_v1()
...     model.calc_alv_arv_ulv_urv_v1()
...     model.calc_alvr_arvr_ulvr_urvr_v1()
...     model.calc_qm_v1()
...     model.calc_qlv_qrv_v1()
...     model.calc_qlvr_qrvr_v1()
...     model.calc_ag_v1()
...     model.calc_qg_v1()
...     error = fluxes.qg[0]-q
...     print_vector([q, h, error])
0.0, -10.0, 0.0
0.000001, -0.390737, 0.0
0.00001, -0.308934, 0.0
0.0001, -0.226779, 0.0
0.001, -0.143209, 0.0
0.01, -0.053833, 0.0
0.1, 0.061356, 0.0
1.0, 0.310079, 0.0
10.0, 1.150307, 0.0
100.0, 3.717833, 0.0
1000.0, 9.108276, 0.0
10000.0, 18.246131, 0.0
100000.0, 37.330632, 0.0
1000000.0, 81.363979, 0.0

Due to smoothing the water stage with respect to the channel bottom, small discharge values result in negative water stages. The lowest allowed stage is -10 m.

Through setting the regularisation parameter HR to zero (which we do not recommend), method Return_H_V1 should return the non-negative water stages agreeing with the original, discontinuous Manning-Strickler equation:

>>> hr(0.0)
>>> parameters.update()
>>> for q in [0.0]+list(numpy.logspace(-6, 6, 13)):
...     fluxes.qg = q
...     h = model.return_h_v1()
...     states.h = h
...     model.calc_rhm_v1()
...     model.calc_rhmdh_v1()
...     model.calc_rhv_v1()
...     model.calc_rhvdh_v1()
...     model.calc_rhlvr_rhrvr_v1()
...     model.calc_rhlvrdh_rhrvrdh_v1()
...     model.calc_am_um_v1()
...     model.calc_alv_arv_ulv_urv_v1()
...     model.calc_alvr_arvr_ulvr_urvr_v1()
...     model.calc_qm_v1()
...     model.calc_qlv_qrv_v1()
...     model.calc_qlvr_qrvr_v1()
...     model.calc_ag_v1()
...     model.calc_qg_v1()
...     error = fluxes.qg[0]-q
...     print_vector([q, h, error])
0.0, 0.0, 0.0
0.000001, 0.00008, 0.0
0.00001, 0.000317, 0.0
0.0001, 0.001263, 0.0
0.001, 0.005027, 0.0
0.01, 0.019992, 0.0
0.1, 0.079286, 0.0
1.0, 0.31039, 0.0
10.0, 1.150307, 0.0
100.0, 3.717833, 0.0
1000.0, 9.108276, 0.0
10000.0, 18.246131, 0.0
100000.0, 37.330632, 0.0
1000000.0, 81.363979, 0.0

class hydpy.models.kinw.kinw_model.PegasusH(model: Model)[source]¶

Bases: Pegasus

Pegasus iterator for finding the correct water stage.

METHODS: ClassVar[tuple[type[Method], ...]] = (<class 'hydpy.models.kinw.kinw_model.Return_QF_V1'>,)¶

name: ClassVar[str] = 'pegasush'¶

class hydpy.models.kinw.kinw_model.BaseModelProfile[source]¶

Bases: ELSModel

Base class for HydPy-KinW models performing discharge calculations based on a triple trapezoid profile.

plot_profile(labelformat: str = '%.1f')[source]¶

Plot the triple trapezoid profile and insert the discharge values at some distinct stages.

We reuse the second example given in the main documentation on module kinw_williams:

>>> from hydpy.models.kinw_williams import *
>>> parameterstep("1d")
>>> simulationstep("30m")
>>> laen(100.0)
>>> gef(0.00025)
>>> bm(15.0)
>>> bnm(5.0)
>>> skm(1.0/0.035)
>>> hm(6.0)
>>> bv(100.0)
>>> bbv(20.0)
>>> bnv(10.0)
>>> bnvr(100.0)
>>> skv(10.0)
>>> ekm(1.0)
>>> ekv(1.0)
>>> hr(0.1)
>>> gts(1)
>>> parameters.update()

Calling method plot_profile() prepares the profile plot and, depending on your matplotlib configuration, eventually prints it directly on your screen:

>>> model.plot_profile()
>>> from hydpy.core.testtools import save_autofig
>>> save_autofig("kinw_plot_profile.png")

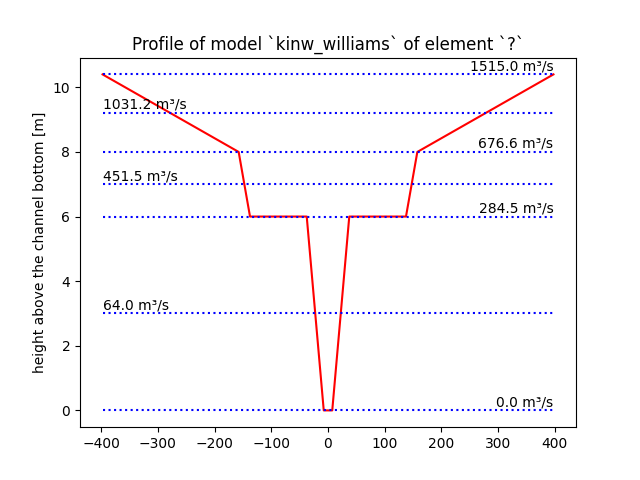
prepare_hvector(nmb: int = 1000, exp: float = 2.0, hmin: float | None = None, hmax: float | None = None) → tuple[float, ...][source]¶

Prepare a vector of the stage values.

The argument nmb defines the number of stage values, exp defines their spacing (1.0 results in equidistant values), and hmin and hmax the lowest and highest water stage, respectively:

>>> from hydpy.models.kinw_williams import *
>>> parameterstep()
>>> from hydpy import print_vector
>>> print_vector(model.prepare_hvector(
...     nmb=10, hmin=-1.0, hmax=8, exp=1.0))
-1.0, 0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0

When not specified by the user, method prepare_hvector() determines hmin and hmax based on the current value of HM (-10 % and 300 %, respectively) and takes a higher sampling rate in the lower value range (by setting exp to two):

>>> hm(6.0)
>>> print_vector(model.prepare_hvector(nmb=10))
-0.6, -0.37037, 0.318519, 1.466667, 3.074074, 5.140741, 7.666667,
10.651852, 14.096296, 18.0

calculate_qgvector(hvector: Iterable[float]) → tuple[float, ...][source]¶

Calculate the discharge values (in m³/s) corresponding to the given stage vector.

We reuse the second example given in the main documentation on module kinw_williams also show the results of the similar methods calculate_agvector() and calculate_vgvector():

>>> from hydpy.models.kinw_williams import *
>>> parameterstep("1d")
>>> simulationstep("30m")
>>> laen(100.0)
>>> gef(0.00025)
>>> bm(15.0)
>>> bnm(5.0)
>>> skm(1.0/0.035)
>>> hm(6.0)
>>> bv(100.0)
>>> bbv(20.0)
>>> bnv(10.0)
>>> bnvr(100.0)
>>> skv(10.0)
>>> ekm(1.0)
>>> ekv(1.0)
>>> hr(0.1)
>>> gts(2)
>>> parameters.update()

>>> from hydpy import print_vector
>>> print_vector(model.calculate_qgvector([0.0, 1.0, 2.0]))
0.033153, 7.745345, 28.436875
>>> print_vector(model.calculate_agvector([0.0, 1.0, 2.0]))
0.623138, 20.0, 50.0
>>> print_vector(model.calculate_vgvector([0.0, 1.0, 2.0]))
0.031157, 1.0, 2.5

calculate_agvector(hvector: Iterable[float]) → tuple[float, ...][source]¶

Calculate the wetted cross-section areas (in m²) corresponding to the given vector of stage values.

See the documentation on method calculate_qgvector() for an example.

REUSABLE_METHODS: ClassVar[tuple[type[ReusableMethod], ...]] = ()¶

calculate_vgvector(hvector: Iterable[float]) → tuple[float, ...][source]¶

Calculate the water volume stored within a channel subsection (in Mio m³) corresponding to the given vector of stage values.

See the documentation on method calculate_qgvector() for an example.

Parameter Features¶

Control parameters¶

class hydpy.models.kinw.ControlParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Control parameters of model kinw.

The following classes are selected:

Laen() Flusslänge (channel length) [km].
Length() Channel length [km].
Gef() Sohlgefälle (channel slope) [-].
GTS() Anzahl Gewässerteilstrecken (number of channel subsections) [-].
NmbSegments() Number of channel segments [-].
HM() Höhe Hauptgerinne (height of the main channel) [m].
BM() Sohlbreite Hauptgerinne (bed width of the main channel) [m].
BNM() Böschungsneigung Hauptgerinne (slope of both main channel embankments) [-].
BV() Sohlbreite Vorländer (bed widths of both forelands) [m].
BBV() Breite Vorlandböschungen (width of both foreland embankments) [m].
BNV() Böschungsneigung Vorländer (slope of both foreland embankments) [-].
BNVR() Böschungsneigung Vorlandränder (slope of both outer embankments) [-].
SKM() Rauigkeitsbeiwert Hauptgerinne (roughness coefficient of the main channel) [m^(1/3)/s].
SKV() Rauigkeitsbeiwert Vorländer (roughness coefficient of both forelands) [m^(1/3)/s].
EKM() Kalibrierfaktor Hauptgerinne (calibration factor for the main channel) [-].
EKV() Kalibrierfaktor Vorländer (calibration factor for both forelands) [m].
HR() Allgemeiner Glättungsparameter für den Wasserstand (general smoothing parameter for the water stage) [mm].
VG2FG() Flexibler Interpolator zur Berechnung der Fließgeschwindigkeit in Abhängigkeit zur aktuellen Wasserspeicherung einer Gewässerteilstrecke (flexible interpolator describing the relationship between the flow velocity and the water storage of individual channel subsections) [m/s].
EK() Kalibrierfaktor (calibration factor) [-].

class hydpy.models.kinw.kinw_control.Laen(subvars: SubParameters)[source]¶

Bases: Parameter

Flusslänge (channel length) [km].

Required by the methods:: Calc_DH_V1 Calc_QG_V2

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'laen'¶: Name of the variable in lowercase letters.

unit: str = 'km'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.Length(subvars: SubParameters)[source]¶

Bases: Parameter

Channel length [km].

Required by the methods:: Calc_WaterDepth_V1 Return_InitialWaterVolume_V1 Return_VolumeError_V1 Update_WaterVolume_V2

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'length'¶: Name of the variable in lowercase letters.

unit: str = 'km'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.Gef(subvars: SubParameters)[source]¶

Bases: Parameter

Sohlgefälle (channel slope) [-].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'gef'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.GTS(subvars: SubParameters)[source]¶

Bases: Parameter

Anzahl Gewässerteilstrecken (number of channel subsections) [-].

Required by the methods:
Calc_AG_V1 Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_ALVR_ARVR_ULVR_URVR_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_AMDH_UMDH_V1 Calc_AM_UM_V1 Calc_DH_V1 Calc_QA_V1 Calc_QG_V1 Calc_QG_V2 Calc_QLVDH_QRVDH_V1 Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V1 Calc_QLVR_QRVR_V2 Calc_QLV_QRV_V1 Calc_QLV_QRV_V2 Calc_QMDH_V1 Calc_QM_V1 Calc_QM_V2 Calc_RHLVRDH_RHRVRDH_V1 Calc_RHLVR_RHRVR_V1 Calc_RHMDH_V1 Calc_RHM_V1 Calc_RHVDH_V1 Calc_RHV_V1 Calc_WBG_V1 Calc_WBLVR_WBRVR_V1 Calc_WBLV_WBRV_V1 Calc_WBM_V1 Return_H_V1 Return_QF_V1 Update_H_V1 Update_VG_V1

Calling the parameter GTS prepares the shape of all 1-dimensional sequences for which each entry corresponds to an individual channel subsection:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> gts(3)
>>> states.h
h(nan, nan, nan)

NDIM: int = 0¶

TYPE¶: alias of int

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0, None)¶

name: str = 'gts'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.NmbSegments(subvars: SubParameters)[source]¶

Bases: NmbParameter

Number of channel segments [-].

Required by the methods:
Calc_InternalFlow_Outflow_V1 Calc_Outflow_V1 Calc_WaterDepth_V1 Return_InitialWaterVolume_V1 Return_VolumeError_V1 Update_WaterVolume_V2

NmbSegments prepares the shape of some 1-dimensional sequences automatically:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> nmbsegments(2)
>>> nmbsegments
nmbsegments(2)
>>> states.watervolume.shape
(2,)
>>> factors.waterdepth.shape
(2,)
>>> fluxes.internalflow.shape
(1,)

NmbSegments preserves existing values if the number of segments does not change:

>>> states.watervolume = 1.0, 2.0
>>> nmbsegments(2)
>>> states.watervolume
watervolume(1.0, 2.0)

Setting its value to zero is allowed:

>>> nmbsegments(0)
>>> states.watervolume.shape
(0,)
>>> fluxes.internalflow.shape
(0,)

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0, None)¶

name: str = 'nmbsegments'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.HM(subvars: SubParameters)[source]¶

Bases: Parameter

Höhe Hauptgerinne (height of the main channel) [m].

Required by the methods:: Calc_RHLVRDH_RHRVRDH_V1 Calc_RHLVR_RHRVR_V1 Calc_RHVDH_V1 Calc_RHV_V1 Return_H_V1 Return_QF_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'hm'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.BM(subvars: SubParameters)[source]¶

Bases: Parameter

Sohlbreite Hauptgerinne (bed width of the main channel) [m].

Required by the methods:: Calc_AMDH_UMDH_V1 Calc_AM_UM_V1 Calc_WBM_V1 Return_H_V1 Return_QF_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'bm'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.BNM(subvars: SubParameters)[source]¶

Bases: Parameter

Böschungsneigung Hauptgerinne (slope of both main channel embankments) [-].

Required by the methods:: Calc_AMDH_UMDH_V1 Calc_AM_UM_V1 Calc_WBM_V1 Return_H_V1 Return_QF_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'bnm'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.BV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Sohlbreite Vorländer (bed widths of both forelands) [m].

Required by the methods:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_WBLV_WBRV_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'bv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.BBV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Breite Vorlandböschungen (width of both foreland embankments) [m].

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'bbv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.BNV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Böschungsneigung Vorländer (slope of both foreland embankments) [-].

Required by the methods:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_WBLV_WBRV_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'bnv'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.BNVR(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Böschungsneigung Vorlandränder (slope of both outer embankments) [-].

Required by the methods:: Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_ALVR_ARVR_ULVR_URVR_V1 Calc_WBLVR_WBRVR_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'bnvr'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.SKM(subvars: SubParameters)[source]¶

Bases: Parameter

Rauigkeitsbeiwert Hauptgerinne (roughness coefficient of the main channel) [m^(1/3)/s].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'skm'¶: Name of the variable in lowercase letters.

unit: str = 'm^(1/3)/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.SKV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Rauigkeitsbeiwert Vorländer (roughness coefficient of both forelands) [m^(1/3)/s].

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'skv'¶: Name of the variable in lowercase letters.

unit: str = 'm^(1/3)/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.EKM(subvars: SubParameters)[source]¶

Bases: Parameter

Kalibrierfaktor Hauptgerinne (calibration factor for the main channel) [-].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ekm'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.EKV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Kalibrierfaktor Vorländer (calibration factor for both forelands) [m].

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ekv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.HR(subvars: SubParameters)[source]¶

Bases: Parameter

Allgemeiner Glättungsparameter für den Wasserstand (general smoothing parameter for the water stage) [mm].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'hr'¶: Name of the variable in lowercase letters.

unit: str = 'mm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_control.VG2FG(subvars: SubParameters)[source]¶

Bases: SimpleInterpolator

Flexibler Interpolator zur Berechnung der Fließgeschwindigkeit in Abhängigkeit zur aktuellen Wasserspeicherung einer Gewässerteilstrecke (flexible interpolator describing the relationship between the flow velocity and the water storage of individual channel subsections) [m/s].

Required by the method:
Calc_QG_V2

You can configure the velocity-storage relationship with all functionalities provided by classes ANN and PPoly. Here, we define a small neural network:

>>> from hydpy.models.kinw import *
>>> parameterstep()
>>> vg2fg(ANN(weights_input=-1.0, weights_output=0.4,
...           intercepts_hidden=0.0, intercepts_output=0.2))
>>> vg2fg
vg2fg(
    ANN(
        weights_input=[[-1.0]],
        weights_output=[[0.4]],
        intercepts_hidden=[[0.0]],
        intercepts_output=[0.2],
    )
)
>>> vg2fg.print_table([0.0, 1.0, inf])
x    y         dy/dx
0.0  0.4       -0.1
1.0  0.307577  -0.078645
inf  0.2       0.0

If you prefer a constant velocity, you can set it directly via the keyword velocity (its unit must be m/s):

>>> vg2fg(velocity=1.0)
>>> vg2fg
vg2fg(velocity=1.0)
>>> vg2fg.print_table([0.0, 1.0])
x    y    dy/dx
0.0  1.0  0.0
1.0  1.0  0.0

Alternatively, the keyword timedelay allows for defining the flow velocity via the number of hours it takes for a flood wave to travel through the whole channel:

>>> laen(100.0)
>>> vg2fg(timedelay=27.77778)
>>> vg2fg
vg2fg(timedelay=27.77778)

>>> vg2fg.inputs[0] = 0.0
>>> vg2fg.calculate_values()
>>> vg2fg.print_table([0.0, 1.0])
x    y    dy/dx
0.0  1.0  0.0
1.0  1.0  0.0

The same time delay indicates a ten times slower flow velocity for a ten times shorter channel:

>>> laen(10.0)
>>> vg2fg(timedelay=27.77778)
>>> vg2fg
vg2fg(timedelay=27.77778)
>>> vg2fg.print_table([0.0, 1.0])
x    y    dy/dx
0.0  0.1  0.0
1.0  0.1  0.0

You must supply precisely one argument:

>>> vg2fg()
Traceback (most recent call last):
...
ValueError: parameter `vg2fg` of element `?` requires exactly one argument but `0` are given.

XLABEL = 'VG [million m³]'¶

YLABEL = 'FG [m/s]'¶

name: str = 'vg2fg'¶: Class name in lowercase letters.

class hydpy.models.kinw.kinw_control.EK(subvars: SubParameters)[source]¶

Bases: Parameter

Kalibrierfaktor (calibration factor) [-].

Required by the method:: Calc_QG_V2

NDIM: int = 0¶

TYPE¶: alias of float

name: str = 'ek'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

Derived parameters¶

class hydpy.models.kinw.DerivedParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Derived parameters of model kinw.

The following classes are selected:

Sek() Sekunden im Simulationszeitschritt (Number of seconds of the selected simulation time step) [s].
Seconds() The length of the actual simulation step size in seconds [s].
HV() Höhe Vorländer (height of both forelands) [m].
MFM() Produkt der zeitkonstanten Terme der Manning-Strickler-Formel für das Hauptgerinne (product of the time-constant terms of the Manning-Strickler equation, calculated for the main channel) [m^(1/3)/s].
MFV() Produkt der zeitkonstanten Terme der Manning-Strickler-Formel für beide Vorländer (product of the time-constant terms of the Manning-Strickler equation, calculated for both forelands) [m^(1/3)/s].
BNMF() Hilfsterm zur Berechnung des benetzten Böschungsumfangs im Hauptgerinne (auxiliary term for the calculation of the wetted perimeter of the slope of the main channel) [m].
BNVF() Hilfsterm zur Berechnung des benetzten Böschungsumfangs der Vorländer (auxiliary term for the calculation of the wetted perimeter of the slope of both forelands) [m].
BNVRF() Hilfsterm zur Berechnung des benetzten Böschungsumfangs der Vorlandränder (auxiliary term for the calculation of the wetted perimeter of the slope of both outer embankments) [m].
HRP() Wasserstand-Regularisierungs-Parameter zur Verwendung in Verbindung mit Regularisierungsfunktion smooth_logistic2() (regularisation parameter for water stage to be used when applying regularisation function smooth_logistic2()) [m].
NmbDiscontinuities() Number of points of discontinuity in the rating curve [-].
FinalDepth2InitialVolume() A pair of the final water depth and the corresponding initial water volume according to the implicit Euler method for each point of discontinuity in the rating curve [m and million m³].

class hydpy.models.kinw.kinw_derived.Sek(subvars: SubParameters)[source]¶

Bases: SecondsParameter

Sekunden im Simulationszeitschritt (Number of seconds of the selected simulation time step) [s].

Required by the methods:
Update_H_V1 Update_VG_V1

name: str = 'sek'¶: Name of the variable in lowercase letters.

unit: str = 's'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.Seconds(subvars: SubParameters)[source]¶

Bases: SecondsParameter

The length of the actual simulation step size in seconds [s].

Required by the methods:: Calc_InternalFlow_Outflow_V1 Calc_WaterDepth_V1 Return_InitialWaterVolume_V1 Return_VolumeError_V1 Update_WaterVolume_V1

name: str = 'seconds'¶: Name of the variable in lowercase letters.

unit: str = 's'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.HV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Höhe Vorländer (height of both forelands) [m].

Required by the methods:: Calc_RHLVRDH_RHRVRDH_V1 Calc_RHLVR_RHRVR_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Update based on \(HV=BBV/BNV\).

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> bbv(left=10., right=40.)
>>> bnv(left=10., right=20.)
>>> derived.hv.update()
>>> derived.hv
hv(left=1.0, right=2.0)
>>> bbv(left=10., right=0.)
>>> bnv(left=0., right=20.)
>>> derived.hv.update()
>>> derived.hv
hv(0.0)

name: str = 'hv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.MFM(subvars: SubParameters)[source]¶

Bases: Parameter

Produkt der zeitkonstanten Terme der Manning-Strickler-Formel für das Hauptgerinne (product of the time-constant terms of the Manning-Strickler equation, calculated for the main channel) [m^(1/3)/s].

Required by the methods:
Calc_QMDH_V1 Calc_QM_V1 Return_H_V1 Return_QF_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Update based on \(MFM=EKM \cdot SKM \cdot \sqrt{Gef}\).

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> ekm(2.0)
>>> skm(50.0)
>>> gef(0.01)
>>> derived.mfm.update()
>>> derived.mfm
mfm(10.0)

name: str = 'mfm'¶: Name of the variable in lowercase letters.

unit: str = 'm^(1/3)/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.MFV(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Produkt der zeitkonstanten Terme der Manning-Strickler-Formel für beide Vorländer (product of the time-constant terms of the Manning-Strickler equation, calculated for both forelands) [m^(1/3)/s].

Required by the methods:
Calc_QLVDH_QRVDH_V1 Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V1 Calc_QLV_QRV_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Update based on \(MFV=EKV \cdot SKV \cdot \sqrt{Gef}\).

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> ekv(left=2.0, right=4.0)
>>> skv(left=25.0, right=50)
>>> gef(0.01)
>>> derived.mfv.update()
>>> derived.mfv
mfv(left=5.0, right=20.0)

name: str = 'mfv'¶: Name of the variable in lowercase letters.

unit: str = 'm^(1/3)/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.BNMF(subvars: SubParameters)[source]¶

Bases: Parameter

Hilfsterm zur Berechnung des benetzten Böschungsumfangs im Hauptgerinne (auxiliary term for the calculation of the wetted perimeter of the slope of the main channel) [m].

Required by the methods:
Calc_AMDH_UMDH_V1 Calc_AM_UM_V1 Return_H_V1 Return_QF_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Update based on \(BNMF= \sqrt{1+BNM^2}\).

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> bnm(2.0)
>>> derived.bnmf.update()
>>> derived.bnmf
bnmf(2.236068)

name: str = 'bnmf'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.BNVF(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Hilfsterm zur Berechnung des benetzten Böschungsumfangs der Vorländer (auxiliary term for the calculation of the wetted perimeter of the slope of both forelands) [m].

Required by the methods:
Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALV_ARV_ULV_URV_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Update based on \(BNVF= \sqrt{1+BNV^2}\).

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> bnv(left=2.0, right=3.0)
>>> derived.bnvf.update()
>>> derived.bnvf
bnvf(left=2.236068, right=3.162278)

name: str = 'bnvf'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.BNVRF(subvars: SubParameters)[source]¶

Bases: LeftRightParameter

Hilfsterm zur Berechnung des benetzten Böschungsumfangs der Vorlandränder (auxiliary term for the calculation of the wetted perimeter of the slope of both outer embankments) [m].

Required by the methods:
Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_ALVR_ARVR_ULVR_URVR_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Update based on \(BNVRF= \sqrt(1+BNVR^2)\).

Examples:

>>> from hydpy.models.kinw import *
>>> parameterstep("1d")
>>> bnvr(left=2.0, right=3.0)
>>> derived.bnvrf.update()
>>> derived.bnvrf
bnvrf(left=2.236068, right=3.162278)

name: str = 'bnvrf'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.HRP(subvars: SubParameters)[source]¶

Bases: Parameter

Wasserstand-Regularisierungs-Parameter zur Verwendung in Verbindung mit Regularisierungsfunktion smooth_logistic2() (regularisation parameter for water stage to be used when applying regularisation function smooth_logistic2()) [m].

Required by the methods:
Calc_RHLVRDH_RHRVRDH_V1 Calc_RHLVR_RHRVR_V1 Calc_RHMDH_V1 Calc_RHM_V1 Calc_RHVDH_V1 Calc_RHV_V1 Return_H_V1 Return_QF_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Calculate the smoothing parameter value.

The documentation on module smoothtools explains the following example in some detail:

>>> from hydpy.models.kinw import *
>>> from hydpy.cythons.smoothutils import smooth_logistic2
>>> from hydpy import round_
>>> parameterstep()
>>> hr(0.0)
>>> derived.hrp.update()
>>> round_(smooth_logistic2(0.0, derived.hrp))
0.0
>>> hr(2.5)
>>> derived.hrp.update()
>>> round_(smooth_logistic2(2.5, derived.hrp))
2.51

name: str = 'hrp'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.NmbDiscontinuities(subvars: SubParameters)[source]¶

Bases: Parameter

Number of points of discontinuity in the rating curve [-].

Required by the method:: Calc_WaterDepth_V1

NDIM: int = 0¶

TYPE¶: alias of int

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0, None)¶

update()[source]¶

Take the number of discontinuities from the available cross-section submodel.

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(2)
...     bottomlevels(1.0, 3.0)
...     bottomslope(0.01)
...     sideslopes(2.0, 4.0)
...     calibrationfactors(1.0)
>>> derived.nmbdiscontinuities.update()
>>> derived.nmbdiscontinuities
nmbdiscontinuities(1)

name: str = 'nmbdiscontinuities'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_derived.FinalDepth2InitialVolume(subvars: SubParameters)[source]¶

Bases: Parameter

A pair of the final water depth and the corresponding initial water volume according to the implicit Euler method for each point of discontinuity in the rating curve [m and million m³].

Required by the method:
Calc_WaterDepth_V1

NDIM: int = 2¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

update()[source]¶

Use the methods get_depths_of_discontinuity() and Return_InitialWaterVolume_V1 to determine the final water depths and the corresponding initial water volumes.

>>> from hydpy.models.kinw_impl_euler import *
>>> parameterstep()
>>> length(100.0)
>>> nmbsegments(10)
>>> derived.seconds(60 * 60 * 24)
>>> with model.add_wqmodel_v1("wq_trapeze_strickler"):
...     nmbtrapezes(3)
...     bottomlevels(1.0, 3.0, 5.0)
...     bottomwidths(20.0)
...     sideslopes(0.0, 0.0, 0.0)
...     bottomslope(0.001)
...     stricklercoefficients(30.0)
...     calibrationfactors(1.0)
>>> derived.nmbdiscontinuities.update()
>>> derived.finaldepth2initialvolume.update()
>>> derived.finaldepth2initialvolume
finaldepth2initialvolume([[2.0, 5.008867],
                          [4.0, 19.01208]])

name: str = 'finaldepth2initialvolume'¶: Name of the variable in lowercase letters.

unit: str = 'm and million m³'¶: Unit of the variable.

Fixed parameters¶

class hydpy.models.kinw.FixedParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Fixed parameters of model kinw.

The following classes are selected:

WBMin() Mindestwert der Wasserspiegelbreite (minimum value of the water level width [m].
WBReg() Auf WBMin bezogener effektiver Glättungsparameter (effectiv smoothing parameter related to WBMin) [m].

class hydpy.models.kinw.kinw_fixed.WBMin(subvars: SubParameters)[source]¶

Bases: FixedParameter

Mindestwert der Wasserspiegelbreite (minimum value of the water level width [m].

Required by the method:
Calc_WBM_V1

In theory, the value of WBMin should always be zero. However, at least the numerical implementation of application model kinw_williams requires a value slightly lower than zero for reasons of numerical stability when the simulated river section is dry.

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 1e-09¶

name: str = 'wbmin'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fixed.WBReg(subvars: SubParameters)[source]¶

Bases: FixedParameter

Auf WBMin bezogener effektiver Glättungsparameter (effectiv smoothing parameter related to WBMin) [m].

Required by the method:
Calc_WBM_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 1e-05¶

name: str = 'wbreg'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

Solver parameters¶

class hydpy.models.kinw.SolverParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Solver parameters of model kinw.

The following classes are selected:

NmbRuns() The number of (repeated) runs of the RUN_METHODS per simulation step [-].
AbsErrorMax() Absolute numerical error tolerance [m³/s].
RelErrorMax() Relative numerical error tolerance [-].
RelDTMin() Smallest relative integration time step size allowed [-].
RelDTMax() Largest relative integration time step size allowed [-].
WaterVolumeTolerance() Targeted accuracy in terms of the relative water volume for the Pegasus search of the final water depth [-].
WaterDepthTolerance() Targeted accuracy in terms of the absolute water depth for the Pegasus search of the final water depth [m].

class hydpy.models.kinw.kinw_solver.NmbRuns(subvars)[source]¶

Bases: SolverParameter

The number of (repeated) runs of the RUN_METHODS per simulation step [-].

NDIM: int = 0¶

TYPE¶: alias of int

TIME: bool | None = None¶

INIT: int | float | bool = 1¶

name: str = 'nmbruns'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_solver.AbsErrorMax(subvars)[source]¶

Bases: SolverParameter

Absolute numerical error tolerance [m³/s].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 1e-06¶

name: str = 'abserrormax'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_solver.RelErrorMax(subvars)[source]¶

Bases: SolverParameter

Relative numerical error tolerance [-].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 0.001¶

name: str = 'relerrormax'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_solver.RelDTMin(subvars)[source]¶

Bases: SolverParameter

Smallest relative integration time step size allowed [-].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 0.0¶

name: str = 'reldtmin'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_solver.RelDTMax(subvars)[source]¶

Bases: SolverParameter

Largest relative integration time step size allowed [-].

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, 1.0)¶

INIT: int | float | bool = 1.0¶

name: str = 'reldtmax'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_solver.WaterVolumeTolerance(subvars)[source]¶

Bases: SolverParameter

Targeted accuracy in terms of the relative water volume for the Pegasus search of the final water depth [-].

Required by the method:
Calc_WaterDepth_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 1e-10¶

name: str = 'watervolumetolerance'¶: Name of the variable in lowercase letters.

unit: str = '-'¶: Unit of the variable.

class hydpy.models.kinw.kinw_solver.WaterDepthTolerance(subvars)[source]¶

Bases: SolverParameter

Targeted accuracy in terms of the absolute water depth for the Pegasus search of the final water depth [m].

Required by the method:
Calc_WaterDepth_V1

NDIM: int = 0¶

TYPE¶: alias of float

TIME: bool | None = None¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

INIT: int | float | bool = 1e-10¶

name: str = 'waterdepthtolerance'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

Sequence Features¶

Factor sequences¶

class hydpy.models.kinw.FactorSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: FactorSequences

Factor sequences of model kinw.

The following classes are selected:

WaterDepth() Water depth [m].

class hydpy.models.kinw.kinw_factors.WaterDepth(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FactorSequence

Water depth [m].

Calculated by the method:: Calc_WaterDepth_V1
Required by the method:: Update_WaterVolume_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'waterdepth'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

Flux sequences¶

class hydpy.models.kinw.FluxSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: FluxSequences

Flux sequences of model kinw.

The following classes are selected:

QZ() Mittlerer Zufluss in Gerinnestrecke (average inflow into the channel) [m³/s].
QZA() Aktueller Zufluss in Gerinnestrecke (current inflow into the channel) [m³/s].
Inflow() Flow into the first channel segment [m³/s].
QG() Durchfluss gesamt (total discharge) [m³/s].
InternalFlow() Flow between the channel segments [m³/s].
QA() Abfluss aus Gerinnestrecke (outflow out of the channel) [m³/s].
Outflow() Flow out of the last channel segment [m³/s].
DH() Wasserstandänderung (temporal change of the water stage) [m/s].

class hydpy.models.kinw.kinw_fluxes.QZ(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Mittlerer Zufluss in Gerinnestrecke (average inflow into the channel) [m³/s].

Calculated by the method:
Pick_Q_V1

Required by the methods:
Calc_DH_V1 Calc_QA_V1

NDIM: int = 0¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qz'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.QZA(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Aktueller Zufluss in Gerinnestrecke (current inflow into the channel) [m³/s].

Required by the method:
Update_VG_V1

NDIM: int = 0¶

NUMERIC: bool = True¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qza'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.Inflow(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Flow into the first channel segment [m³/s].

Calculated by the method:: Pick_Inflow_V1
Required by the methods:: Calc_Outflow_V1 Update_WaterVolume_V1

NDIM: int = 0¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (None, None)¶

name: str = 'inflow'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.QG(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Durchfluss gesamt (total discharge) [m³/s].

Calculated by the methods:: Calc_QG_V1 Calc_QG_V2
Required by the methods:: Calc_DH_V1 Calc_QA_V1 Update_VG_V1

NDIM: int = 1¶

NUMERIC: bool = True¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qg'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.InternalFlow(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Flow between the channel segments [m³/s].

Calculated by the method:: Calc_InternalFlow_Outflow_V1
Required by the method:: Update_WaterVolume_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (None, None)¶

name: str = 'internalflow'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.QA(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Abfluss aus Gerinnestrecke (outflow out of the channel) [m³/s].

Calculated by the method:: Calc_QA_V1
Required by the method:: Pass_Q_V1

NDIM: int = 0¶

NUMERIC: bool = True¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qa'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.Outflow(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Flow out of the last channel segment [m³/s].

Calculated by the methods:: Calc_InternalFlow_Outflow_V1 Calc_Outflow_V1
Required by the method:: Pass_Outflow_V1

NDIM: int = 0¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (None, None)¶

name: str = 'outflow'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_fluxes.DH(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: FluxSequence

Wasserstandänderung (temporal change of the water stage) [m/s].

Calculated by the method:: Calc_DH_V1
Required by the method:: Update_H_V1

NDIM: int = 1¶

NUMERIC: bool = True¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'dh'¶: Name of the variable in lowercase letters.

unit: str = 'm/s'¶: Unit of the variable.

State sequences¶

class hydpy.models.kinw.StateSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: StateSequences

State sequences of model kinw.

The following classes are selected:

H() Wasserstand (water stage) [m].
VG() Wasservolumen (water volume) [million m³].
WaterVolume() Water volume [million m³].

class hydpy.models.kinw.kinw_states.H(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: StateSequence

Wasserstand (water stage) [m].

Calculated by the methods:: Return_H_V1 Return_QF_V1
Updated by the method:: Update_H_V1
Required by the methods:: Calc_RHLVRDH_RHRVRDH_V1 Calc_RHLVR_RHRVR_V1 Calc_RHMDH_V1 Calc_RHM_V1 Calc_RHVDH_V1 Calc_RHV_V1

NDIM: int = 1¶

NUMERIC: bool = True¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (None, None)¶

name: str = 'h'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_states.VG(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: StateSequence

Wasservolumen (water volume) [million m³].

Updated by the method:: Update_VG_V1
Required by the method:: Calc_QG_V2

NDIM: int = 1¶

NUMERIC: bool = True¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (None, None)¶

name: str = 'vg'¶: Name of the variable in lowercase letters.

unit: str = 'million m³'¶: Unit of the variable.

class hydpy.models.kinw.kinw_states.WaterVolume(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: StateSequence

Water volume [million m³].

Updated by the methods:: Update_WaterVolume_V1 Update_WaterVolume_V2
Required by the methods:: Calc_InternalFlow_Outflow_V1 Calc_WaterDepth_V1 Return_VolumeError_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'watervolume'¶: Name of the variable in lowercase letters.

unit: str = 'million m³'¶: Unit of the variable.

Inlet sequences¶

class hydpy.models.kinw.InletSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: InletSequences

Inlet sequences of model kinw.

The following classes are selected:

Q() Abfluss (runoff) [m³/s].

class hydpy.models.kinw.kinw_inlets.Q(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: InletSequence

Abfluss (runoff) [m³/s].

Required by the methods:: Pick_Inflow_V1 Pick_Q_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

name: str = 'q'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

Outlet sequences¶

class hydpy.models.kinw.OutletSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: OutletSequences

Outlet sequences of model kinw.

The following classes are selected:

Q() Abfluss (runoff) [m³/s].

class hydpy.models.kinw.kinw_outlets.Q(subvars: ModelIOSequences[ModelIOSequence, FastAccessIOSequence])[source]¶

Bases: OutletSequence

Abfluss (runoff) [m³/s].

Calculated by the methods:: Pass_Outflow_V1 Pass_Q_V1

NDIM: int = 0¶

NUMERIC: bool = False¶

name: str = 'q'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

Aide sequences¶

class hydpy.models.kinw.AideSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: AideSequences

Aide sequences of model kinw.

The following classes are selected:

WBM() Wasserspiegelbreite Hauptgerinne (water level width of the main channel) [m].
WBLV() Wasserspiegelbreite des linken Vorlandes (water level width of the left foreland) [m].
WBRV() Wasserspiegelbreite des rechten Vorlandes (water level width of the right foreland) [m].
WBLVR() Wasserspiegelbreite des linken Vorlandrandes (water level width of the left outer embankment) [m].
WBRVR() Wasserspiegelbreite des rechten Vorlandrandes (water level width of the right outer embankment) [m].
WBG() Wasserspiegelbreite des gesamten Querschnittes (water level width of the total cross section) [m].
AM() Durchflossene Fläche Hauptgerinne (wetted area of the main channel) [m²].
ALV() Durchflossene Fläche linkes Vorland (wetted area of the left foreland) [m²].
ARV() Durchflossene Fläche rechtes Vorland (wetted area of the right foreland) [m²].
ALVR() Durchflossene Fläche linker Vorlandrand (wetted area of the left outer embankments) [m²].
ARVR() Durchflossene Fläche rechter Vorlandrand (wetted area of the right outer embankments) [m²].
AG() Durchflossene Fläche gesamt (total wetted area) [m²].
UM() Benetzter Umfang Hauptgerinne (wetted perimeter of the main channel) [m].
ULV() Benetzter Umfang linkes Vorland (wetted perimeter of the left foreland) [m].
URV() Benetzter Umfang rechtes Vorland (wetted perimeter of the right foreland) [m].
ULVR() Benetzter Umfang linker Vorlandrand (wetted perimeter of the left outer embankment) [m].
URVR() Benetzter Umfang rechtes Vorlandrand (wetted perimeter of the right outer embankment) [m].
QM() Durchfluss Hauptgerinne (discharge of the main channel) [m³/s].
QLV() Durchfluss linkes Vorland (discharge of the left foreland) [m³/s].
QRV() Durchfluss rechtes Vorland (discharge of the right foreland) [m³/s].
QLVR() Durchfluss linker Vorlandrand (discharge of the left outer embankment) [m³/s].
QRVR() Durchfluss rechter Vorlandrand (discharge of the right outer embankment) [m³/s].
RHM() Hinsichtlich der Gewässersohle regularisierter Wasserstand (stage regularised with respect to the channel bottom) [m].
RHMDH() Ableitung von RHM (derivative of RHM) [m/m].
RHV() Hinsichtlich der des Übergangs Hauptgerinne/Vorländer regularisierter Wasserstand (stage regularised with respect to the transition from the main channel to both forelands) [m].
RHVDH() Ableitung von RHV (derivative of RHV) [m/m].
RHLVR() Hinsichtlich der des Übergangs linkes Vorland/ linker Vorlandrand regularisierter Wasserstand (stage regularised with respect to the transition from the left foreland to the left outer embankment) [m].
RHLVRDH() Ableitung von RHLVR (derivative of RHLVR) [m/m].
RHRVR() Hinsichtlich der des Übergangs rechtes Vorland/ rechter Vorlandrand regularisierter Wasserstand (stage regularised with respect to the transition from the right foreland to the right outer embankment) [m].
RHRVRDH() Ableitung von RHRVR (derivative of RHRVR) [m/m].
AMDH() Ableitung von AM (derivative of AM) [m²/m].
ALVDH() Ableitung von ALV (derivative of ALV) [m²/m].
ARVDH() Ableitung von ARV (derivative of ARV) [m²/m].
ALVRDH() Ableitung von ALVR (derivative of ALVR) [m²/m].
ARVRDH() Ableitung von ARVR (derivative of ARVR) [m²/m].
UMDH() Ableitung von UM (derivative of UM) [m/m].
ULVDH() Ableitung von ULV (derivative of ULV) [m/m].
URVDH() Ableitung von URV (derivative of URV) [m/m].
ULVRDH() Ableitung von ULVR (derivative of ULVR) [m/m].
URVRDH() Ableitung von URVR (derivative of URVR) [m/m].
QMDH() Ableitung von QM (derivative of QM) [m³/m].
QLVDH() Ableitung von QLV (derivative of QLV) [m³/m].
QRVDH() Ableitung von QRV (derivative of QRV) [m³/m].
QLVRDH() Ableitung von QLVR (derivative of QLVR) [m³/m].
QRVRDH() Ableitung von QRVR (derivative of QRVR) [m³/m].

class hydpy.models.kinw.kinw_aides.WBM(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Wasserspiegelbreite Hauptgerinne (water level width of the main channel) [m].

Calculated by the method:
Calc_WBM_V1

Required by the method:
Calc_WBG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'wbm'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.WBLV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Wasserspiegelbreite des linken Vorlandes (water level width of the left foreland) [m].

Calculated by the method:
Calc_WBLV_WBRV_V1

Required by the method:
Calc_WBG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'wblv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.WBRV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Wasserspiegelbreite des rechten Vorlandes (water level width of the right foreland) [m].

Calculated by the method:
Calc_WBLV_WBRV_V1

Required by the method:
Calc_WBG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'wbrv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.WBLVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Wasserspiegelbreite des linken Vorlandrandes (water level width of the left outer embankment) [m].

Calculated by the method:
Calc_WBLVR_WBRVR_V1

Required by the method:
Calc_WBG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'wblvr'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.WBRVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Wasserspiegelbreite des rechten Vorlandrandes (water level width of the right outer embankment) [m].

Calculated by the method:
Calc_WBLVR_WBRVR_V1

Required by the method:
Calc_WBG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'wbrvr'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.WBG(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Wasserspiegelbreite des gesamten Querschnittes (water level width of the total cross section) [m].

Calculated by the method:
Calc_WBG_V1

Required by the method:
Calc_DH_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'wbg'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.AM(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchflossene Fläche Hauptgerinne (wetted area of the main channel) [m²].

Calculated by the methods:
Calc_AM_UM_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_AG_V1 Calc_QMDH_V1 Calc_QM_V1 Calc_QM_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'am'¶: Name of the variable in lowercase letters.

unit: str = 'm²'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ALV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchflossene Fläche linkes Vorland (wetted area of the left foreland) [m²].

Calculated by the methods:
Calc_ALV_ARV_ULV_URV_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_AG_V1 Calc_QLVDH_QRVDH_V1 Calc_QLV_QRV_V1 Calc_QLV_QRV_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'alv'¶: Name of the variable in lowercase letters.

unit: str = 'm²'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ARV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchflossene Fläche rechtes Vorland (wetted area of the right foreland) [m²].

Calculated by the methods:
Calc_ALV_ARV_ULV_URV_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_AG_V1 Calc_QLVDH_QRVDH_V1 Calc_QLV_QRV_V1 Calc_QLV_QRV_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'arv'¶: Name of the variable in lowercase letters.

unit: str = 'm²'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ALVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchflossene Fläche linker Vorlandrand (wetted area of the left outer embankments) [m²].

Calculated by the methods:
Calc_ALVR_ARVR_ULVR_URVR_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_AG_V1 Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V1 Calc_QLVR_QRVR_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'alvr'¶: Name of the variable in lowercase letters.

unit: str = 'm²'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ARVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchflossene Fläche rechter Vorlandrand (wetted area of the right outer embankments) [m²].

Calculated by the methods:
Calc_ALVR_ARVR_ULVR_URVR_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_AG_V1 Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V1 Calc_QLVR_QRVR_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'arvr'¶: Name of the variable in lowercase letters.

unit: str = 'm²'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.AG(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchflossene Fläche gesamt (total wetted area) [m²].

Calculated by the methods:: Calc_AG_V1 Return_H_V1 Return_QF_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ag'¶: Name of the variable in lowercase letters.

unit: str = 'm²'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.UM(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Benetzter Umfang Hauptgerinne (wetted perimeter of the main channel) [m].

Calculated by the methods:
Calc_AM_UM_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_QMDH_V1 Calc_QM_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'um'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ULV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Benetzter Umfang linkes Vorland (wetted perimeter of the left foreland) [m].

Calculated by the methods:
Calc_ALV_ARV_ULV_URV_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_QLVDH_QRVDH_V1 Calc_QLV_QRV_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ulv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.URV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Benetzter Umfang rechtes Vorland (wetted perimeter of the right foreland) [m].

Calculated by the methods:
Calc_ALV_ARV_ULV_URV_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_QLVDH_QRVDH_V1 Calc_QLV_QRV_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'urv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ULVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Benetzter Umfang linker Vorlandrand (wetted perimeter of the left outer embankment) [m].

Calculated by the methods:
Calc_ALVR_ARVR_ULVR_URVR_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ulvr'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.URVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Benetzter Umfang rechtes Vorlandrand (wetted perimeter of the right outer embankment) [m].

Calculated by the methods:
Calc_ALVR_ARVR_ULVR_URVR_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'urvr'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QM(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchfluss Hauptgerinne (discharge of the main channel) [m³/s].

Calculated by the methods:: Calc_QM_V1 Calc_QM_V2 Return_H_V1 Return_QF_V1
Required by the method:: Calc_QG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qm'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QLV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchfluss linkes Vorland (discharge of the left foreland) [m³/s].

Calculated by the methods:: Calc_QLV_QRV_V1 Calc_QLV_QRV_V2 Return_H_V1 Return_QF_V1
Required by the method:: Calc_QG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qlv'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QRV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchfluss rechtes Vorland (discharge of the right foreland) [m³/s].

Calculated by the methods:: Calc_QLV_QRV_V1 Calc_QLV_QRV_V2 Return_H_V1 Return_QF_V1
Required by the method:: Calc_QG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qrv'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchfluss Vorlandränder (discharge of both outer embankment) [m³/s].

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qvr'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QLVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchfluss linker Vorlandrand (discharge of the left outer embankment) [m³/s].

Calculated by the methods:
Calc_QLVR_QRVR_V1 Calc_QLVR_QRVR_V2 Return_H_V1 Return_QF_V1

Required by the method:
Calc_QG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qlvr'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QRVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Durchfluss rechter Vorlandrand (discharge of the right outer embankment) [m³/s].

Calculated by the methods:
Calc_QLVR_QRVR_V1 Calc_QLVR_QRVR_V2 Return_H_V1 Return_QF_V1

Required by the method:
Calc_QG_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qrvr'¶: Name of the variable in lowercase letters.

unit: str = 'm³/s'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHM(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Hinsichtlich der Gewässersohle regularisierter Wasserstand (stage regularised with respect to the channel bottom) [m].

Calculated by the methods:
Calc_RHM_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_AMDH_UMDH_V1 Calc_AM_UM_V1 Calc_WBM_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhm'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHMDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von RHM (derivative of RHM) [m/m].

Calculated by the methods:: Calc_RHMDH_V1 Return_H_V1 Return_QF_V1
Required by the methods:: Calc_AMDH_UMDH_V1 Calc_WBM_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhmdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHV(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Hinsichtlich der des Übergangs Hauptgerinne/Vorländer regularisierter Wasserstand (stage regularised with respect to the transition from the main channel to both forelands) [m].

Calculated by the methods:
Calc_RHV_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_AMDH_UMDH_V1 Calc_AM_UM_V1 Calc_WBLV_WBRV_V1 Calc_WBM_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhv'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von RHV (derivative of RHV) [m/m].

Calculated by the methods:: Calc_RHVDH_V1 Return_H_V1 Return_QF_V1
Required by the methods:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_AMDH_UMDH_V1 Calc_WBLV_WBRV_V1 Calc_WBM_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHLVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Hinsichtlich der des Übergangs linkes Vorland/ linker Vorlandrand regularisierter Wasserstand (stage regularised with respect to the transition from the left foreland to the left outer embankment) [m].

Calculated by the methods:
Calc_RHLVR_RHRVR_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_ALVR_ARVR_ULVR_URVR_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_WBLVR_WBRVR_V1 Calc_WBLV_WBRV_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhlvr'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHLVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von RHLVR (derivative of RHLVR) [m/m].

Calculated by the methods:: Calc_RHLVRDH_RHRVRDH_V1 Return_H_V1 Return_QF_V1
Required by the methods:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_WBLVR_WBRVR_V1 Calc_WBLV_WBRV_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhlvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHRVR(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Hinsichtlich der des Übergangs rechtes Vorland/ rechter Vorlandrand regularisierter Wasserstand (stage regularised with respect to the transition from the right foreland to the right outer embankment) [m].

Calculated by the methods:
Calc_RHLVR_RHRVR_V1 Return_H_V1 Return_QF_V1

Required by the methods:
Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_ALVR_ARVR_ULVR_URVR_V1 Calc_ALV_ARV_ULV_URV_V1 Calc_WBLVR_WBRVR_V1 Calc_WBLV_WBRV_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhrvr'¶: Name of the variable in lowercase letters.

unit: str = 'm'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.RHRVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von RHRVR (derivative of RHRVR) [m/m].

Calculated by the methods:: Calc_RHLVRDH_RHRVRDH_V1 Return_H_V1 Return_QF_V1
Required by the methods:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1 Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1 Calc_WBLVR_WBRVR_V1 Calc_WBLV_WBRV_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'rhrvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.AMDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von AM (derivative of AM) [m²/m].

Calculated by the method:: Calc_AMDH_UMDH_V1
Required by the methods:: Calc_QMDH_V1 Calc_QM_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'amdh'¶: Name of the variable in lowercase letters.

unit: str = 'm²/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ALVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von ALV (derivative of ALV) [m²/m].

Calculated by the method:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1
Required by the methods:: Calc_QLVDH_QRVDH_V1 Calc_QLV_QRV_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'alvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm²/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ARVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von ARV (derivative of ARV) [m²/m].

Calculated by the method:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1
Required by the methods:: Calc_QLVDH_QRVDH_V1 Calc_QLV_QRV_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'arvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm²/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ALVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von ALVR (derivative of ALVR) [m²/m].

Calculated by the method:: Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1
Required by the methods:: Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'alvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm²/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ARVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von ARVR (derivative of ARVR) [m²/m].

Calculated by the method:: Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1
Required by the methods:: Calc_QLVRDH_QRVRDH_V1 Calc_QLVR_QRVR_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'arvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm²/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.UMDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von UM (derivative of UM) [m/m].

Calculated by the method:: Calc_AMDH_UMDH_V1
Required by the method:: Calc_QMDH_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'umdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ULVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von ULV (derivative of ULV) [m/m].

Calculated by the method:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1
Required by the method:: Calc_QLVDH_QRVDH_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ulvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.URVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von URV (derivative of URV) [m/m].

Calculated by the method:: Calc_ALVDH_ARVDH_ULVDH_URVDH_V1
Required by the method:: Calc_QLVDH_QRVDH_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'urvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.ULVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von ULVR (derivative of ULVR) [m/m].

Calculated by the method:: Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1
Required by the method:: Calc_QLVRDH_QRVRDH_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'ulvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.URVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von URVR (derivative of URVR) [m/m].

Calculated by the method:: Calc_ALVRDH_ARVRDH_ULVRDH_URVRDH_V1
Required by the method:: Calc_QLVRDH_QRVRDH_V1

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'urvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QMDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von QM (derivative of QM) [m³/m].

Calculated by the method:: Calc_QMDH_V1
Required by the method:: Calc_QM_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qmdh'¶: Name of the variable in lowercase letters.

unit: str = 'm³/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QLVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von QLV (derivative of QLV) [m³/m].

Calculated by the method:: Calc_QLVDH_QRVDH_V1
Required by the method:: Calc_QLV_QRV_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qlvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm³/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QRVDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von QRV (derivative of QRV) [m³/m].

Calculated by the method:: Calc_QLVDH_QRVDH_V1
Required by the method:: Calc_QLV_QRV_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qrvdh'¶: Name of the variable in lowercase letters.

unit: str = 'm³/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QLVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von QLVR (derivative of QLVR) [m³/m].

Calculated by the method:: Calc_QLVRDH_QRVRDH_V1
Required by the method:: Calc_QLVR_QRVR_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qlvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm³/m'¶: Unit of the variable.

class hydpy.models.kinw.kinw_aides.QRVRDH(subvars: ModelSequences[ModelSequence, FastAccess])[source]¶

Bases: AideSequence

Ableitung von QRVR (derivative of QRVR) [m³/m].

Calculated by the method:: Calc_QLVRDH_QRVRDH_V1
Required by the method:: Calc_QLVR_QRVR_V2

NDIM: int = 1¶

NUMERIC: bool = False¶

SPAN: tuple[int | float | bool | None, int | float | bool | None] = (0.0, None)¶

name: str = 'qrvrdh'¶: Name of the variable in lowercase letters.

unit: str = 'm³/m'¶: Unit of the variable.

class hydpy.models.kinw.AideSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: AideSequences

Aide sequences of model kinw.

The following classes are selected:

WBM() Wasserspiegelbreite Hauptgerinne (water level width of the main channel) [m].
WBLV() Wasserspiegelbreite des linken Vorlandes (water level width of the left foreland) [m].
WBRV() Wasserspiegelbreite des rechten Vorlandes (water level width of the right foreland) [m].
WBLVR() Wasserspiegelbreite des linken Vorlandrandes (water level width of the left outer embankment) [m].
WBRVR() Wasserspiegelbreite des rechten Vorlandrandes (water level width of the right outer embankment) [m].
WBG() Wasserspiegelbreite des gesamten Querschnittes (water level width of the total cross section) [m].
AM() Durchflossene Fläche Hauptgerinne (wetted area of the main channel) [m²].
ALV() Durchflossene Fläche linkes Vorland (wetted area of the left foreland) [m²].
ARV() Durchflossene Fläche rechtes Vorland (wetted area of the right foreland) [m²].
ALVR() Durchflossene Fläche linker Vorlandrand (wetted area of the left outer embankments) [m²].
ARVR() Durchflossene Fläche rechter Vorlandrand (wetted area of the right outer embankments) [m²].
AG() Durchflossene Fläche gesamt (total wetted area) [m²].
UM() Benetzter Umfang Hauptgerinne (wetted perimeter of the main channel) [m].
ULV() Benetzter Umfang linkes Vorland (wetted perimeter of the left foreland) [m].
URV() Benetzter Umfang rechtes Vorland (wetted perimeter of the right foreland) [m].
ULVR() Benetzter Umfang linker Vorlandrand (wetted perimeter of the left outer embankment) [m].
URVR() Benetzter Umfang rechtes Vorlandrand (wetted perimeter of the right outer embankment) [m].
QM() Durchfluss Hauptgerinne (discharge of the main channel) [m³/s].
QLV() Durchfluss linkes Vorland (discharge of the left foreland) [m³/s].
QRV() Durchfluss rechtes Vorland (discharge of the right foreland) [m³/s].
QLVR() Durchfluss linker Vorlandrand (discharge of the left outer embankment) [m³/s].
QRVR() Durchfluss rechter Vorlandrand (discharge of the right outer embankment) [m³/s].
RHM() Hinsichtlich der Gewässersohle regularisierter Wasserstand (stage regularised with respect to the channel bottom) [m].
RHMDH() Ableitung von RHM (derivative of RHM) [m/m].
RHV() Hinsichtlich der des Übergangs Hauptgerinne/Vorländer regularisierter Wasserstand (stage regularised with respect to the transition from the main channel to both forelands) [m].
RHVDH() Ableitung von RHV (derivative of RHV) [m/m].
RHLVR() Hinsichtlich der des Übergangs linkes Vorland/ linker Vorlandrand regularisierter Wasserstand (stage regularised with respect to the transition from the left foreland to the left outer embankment) [m].
RHLVRDH() Ableitung von RHLVR (derivative of RHLVR) [m/m].
RHRVR() Hinsichtlich der des Übergangs rechtes Vorland/ rechter Vorlandrand regularisierter Wasserstand (stage regularised with respect to the transition from the right foreland to the right outer embankment) [m].
RHRVRDH() Ableitung von RHRVR (derivative of RHRVR) [m/m].
AMDH() Ableitung von AM (derivative of AM) [m²/m].
ALVDH() Ableitung von ALV (derivative of ALV) [m²/m].
ARVDH() Ableitung von ARV (derivative of ARV) [m²/m].
ALVRDH() Ableitung von ALVR (derivative of ALVR) [m²/m].
ARVRDH() Ableitung von ARVR (derivative of ARVR) [m²/m].
UMDH() Ableitung von UM (derivative of UM) [m/m].
ULVDH() Ableitung von ULV (derivative of ULV) [m/m].
URVDH() Ableitung von URV (derivative of URV) [m/m].
ULVRDH() Ableitung von ULVR (derivative of ULVR) [m/m].
URVRDH() Ableitung von URVR (derivative of URVR) [m/m].
QMDH() Ableitung von QM (derivative of QM) [m³/m].
QLVDH() Ableitung von QLV (derivative of QLV) [m³/m].
QRVDH() Ableitung von QRV (derivative of QRV) [m³/m].
QLVRDH() Ableitung von QLVR (derivative of QLVR) [m³/m].
QRVRDH() Ableitung von QRVR (derivative of QRVR) [m³/m].

class hydpy.models.kinw.ControlParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: SubParameters

Control parameters of model kinw.

The following classes are selected:

Laen() Flusslänge (channel length) [km].
Length() Channel length [km].
Gef() Sohlgefälle (channel slope) [-].
GTS() Anzahl Gewässerteilstrecken (number of channel subsections) [-].
NmbSegments() Number of channel segments [-].
HM() Höhe Hauptgerinne (height of the main channel) [m].
BM() Sohlbreite Hauptgerinne (bed width of the main channel) [m].
BNM() Böschungsneigung Hauptgerinne (slope of both main channel embankments) [-].
BV() Sohlbreite Vorländer (bed widths of both forelands) [m].
BBV() Breite Vorlandböschungen (width of both foreland embankments) [m].
BNV() Böschungsneigung Vorländer (slope of both foreland embankments) [-].
BNVR() Böschungsneigung Vorlandränder (slope of both outer embankments) [-].
SKM() Rauigkeitsbeiwert Hauptgerinne (roughness coefficient of the main channel) [m^(1/3)/s].
SKV() Rauigkeitsbeiwert Vorländer (roughness coefficient of both forelands) [m^(1/3)/s].
EKM() Kalibrierfaktor Hauptgerinne (calibration factor for the main channel) [-].
EKV() Kalibrierfaktor Vorländer (calibration factor for both forelands) [m].
HR() Allgemeiner Glättungsparameter für den Wasserstand (general smoothing parameter for the water stage) [mm].
VG2FG() Flexibler Interpolator zur Berechnung der Fließgeschwindigkeit in Abhängigkeit zur aktuellen Wasserspeicherung einer Gewässerteilstrecke (flexible interpolator describing the relationship between the flow velocity and the water storage of individual channel subsections) [m/s].
EK() Kalibrierfaktor (calibration factor) [-].

class hydpy.models.kinw.DerivedParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: SubParameters

Derived parameters of model kinw.

The following classes are selected:

Sek() Sekunden im Simulationszeitschritt (Number of seconds of the selected simulation time step) [s].
Seconds() The length of the actual simulation step size in seconds [s].
HV() Höhe Vorländer (height of both forelands) [m].
MFM() Produkt der zeitkonstanten Terme der Manning-Strickler-Formel für das Hauptgerinne (product of the time-constant terms of the Manning-Strickler equation, calculated for the main channel) [m^(1/3)/s].
MFV() Produkt der zeitkonstanten Terme der Manning-Strickler-Formel für beide Vorländer (product of the time-constant terms of the Manning-Strickler equation, calculated for both forelands) [m^(1/3)/s].
BNMF() Hilfsterm zur Berechnung des benetzten Böschungsumfangs im Hauptgerinne (auxiliary term for the calculation of the wetted perimeter of the slope of the main channel) [m].
BNVF() Hilfsterm zur Berechnung des benetzten Böschungsumfangs der Vorländer (auxiliary term for the calculation of the wetted perimeter of the slope of both forelands) [m].
BNVRF() Hilfsterm zur Berechnung des benetzten Böschungsumfangs der Vorlandränder (auxiliary term for the calculation of the wetted perimeter of the slope of both outer embankments) [m].
HRP() Wasserstand-Regularisierungs-Parameter zur Verwendung in Verbindung mit Regularisierungsfunktion smooth_logistic2() (regularisation parameter for water stage to be used when applying regularisation function smooth_logistic2()) [m].
NmbDiscontinuities() Number of points of discontinuity in the rating curve [-].
FinalDepth2InitialVolume() A pair of the final water depth and the corresponding initial water volume according to the implicit Euler method for each point of discontinuity in the rating curve [m and million m³].

class hydpy.models.kinw.FactorSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: FactorSequences

Factor sequences of model kinw.

The following classes are selected:

WaterDepth() Water depth [m].

class hydpy.models.kinw.FixedParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: SubParameters

Fixed parameters of model kinw.

The following classes are selected:

WBMin() Mindestwert der Wasserspiegelbreite (minimum value of the water level width [m].
WBReg() Auf WBMin bezogener effektiver Glättungsparameter (effectiv smoothing parameter related to WBMin) [m].

class hydpy.models.kinw.FluxSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: FluxSequences

Flux sequences of model kinw.

The following classes are selected:

QZ() Mittlerer Zufluss in Gerinnestrecke (average inflow into the channel) [m³/s].
QZA() Aktueller Zufluss in Gerinnestrecke (current inflow into the channel) [m³/s].
Inflow() Flow into the first channel segment [m³/s].
QG() Durchfluss gesamt (total discharge) [m³/s].
InternalFlow() Flow between the channel segments [m³/s].
QA() Abfluss aus Gerinnestrecke (outflow out of the channel) [m³/s].
Outflow() Flow out of the last channel segment [m³/s].
DH() Wasserstandänderung (temporal change of the water stage) [m/s].

class hydpy.models.kinw.InletSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: InletSequences

Inlet sequences of model kinw.

The following classes are selected:

Q() Abfluss (runoff) [m³/s].

class hydpy.models.kinw.OutletSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: OutletSequences

Outlet sequences of model kinw.

The following classes are selected:

Q() Abfluss (runoff) [m³/s].

class hydpy.models.kinw.SolverParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: SubParameters

Solver parameters of model kinw.

The following classes are selected:

NmbRuns() The number of (repeated) runs of the RUN_METHODS per simulation step [-].
AbsErrorMax() Absolute numerical error tolerance [m³/s].
RelErrorMax() Relative numerical error tolerance [-].
RelDTMin() Smallest relative integration time step size allowed [-].
RelDTMax() Largest relative integration time step size allowed [-].
WaterVolumeTolerance() Targeted accuracy in terms of the relative water volume for the Pegasus search of the final water depth [-].
WaterDepthTolerance() Targeted accuracy in terms of the absolute water depth for the Pegasus search of the final water depth [m].

class hydpy.models.kinw.StateSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)¶

Bases: StateSequences

State sequences of model kinw.

The following classes are selected:

H() Wasserstand (water stage) [m].
VG() Wasservolumen (water volume) [million m³].
WaterVolume() Water volume [million m³].

Table of Contents

Previous topic

Next topic

This Page

Versions

HydPy-KinW (base model)¶

Method Features¶

Parameter Features¶

Control parameters¶

Derived parameters¶

Fixed parameters¶

Solver parameters¶

Sequence Features¶

Factor sequences¶

Flux sequences¶

State sequences¶

Inlet sequences¶

Outlet sequences¶

Aide sequences¶