anntools¶

This module implements rudimentary artificial neural network tools required for some models implemented in the HydPy framework.

The relevant models apply some of the neural network features during simulation runs, which is why we implement these features in the Cython extension module annutils.

Module anntools implements the following members:

ANN Multi-layer feed-forward artificial neural network.

class hydpy.auxs.anntools.ANN(*, nmb_inputs: int = 1, nmb_neurons: tuple[int, ...] = (1,), nmb_outputs: int = 1, weights_input: Sequence[Sequence[float] | ndarray[Any, dtype[float64]]] | ndarray[Any, dtype[float64]] | None = None, weights_output: Sequence[Sequence[float] | ndarray[Any, dtype[float64]]] | ndarray[Any, dtype[float64]] | None = None, weights_hidden: Sequence[Sequence[Sequence[float] | ndarray[Any, dtype[float64]]] | ndarray[Any, dtype[float64]]] | ndarray[Any, dtype[float64]] | None = None, intercepts_hidden: Sequence[Sequence[float] | ndarray[Any, dtype[float64]]] | ndarray[Any, dtype[float64]] | None = None, intercepts_output: Sequence[float] | ndarray[Any, dtype[float64]] | None = None, activation: Sequence[Sequence[int] | ndarray[Any, dtype[int64]]] | ndarray[Any, dtype[int64]] | None = None)[source]¶

Bases: InterpAlgorithm

Multi-layer feed-forward artificial neural network.

By default, class ANN uses the logistic function \(f(x) = \frac{1}{1+exp(-x)}\) to calculate the activation of the hidden layer’s neurons. Alternatively, one can select the identity function \(f(x) = x\) or a variant of the logistic function for filtering specific inputs. See property activation for more information on how to do this.

You can select ANN as the interpolation algorithm used by SimpleInterpolator or one of the interpolation algorithms used by SeasonalInterpolator. Its original purpose was to define arbitrary continuous relationships between the water stored in a dam and the associated water stage (see model dam_v001). However, class ANN can also be applied directly for testing purposes, as shown in the following examples.

First, define the most simple artificial neural network consisting of only one input node, one hidden neuron, and one output node, and pass arbitrary values for the weights and intercepts:

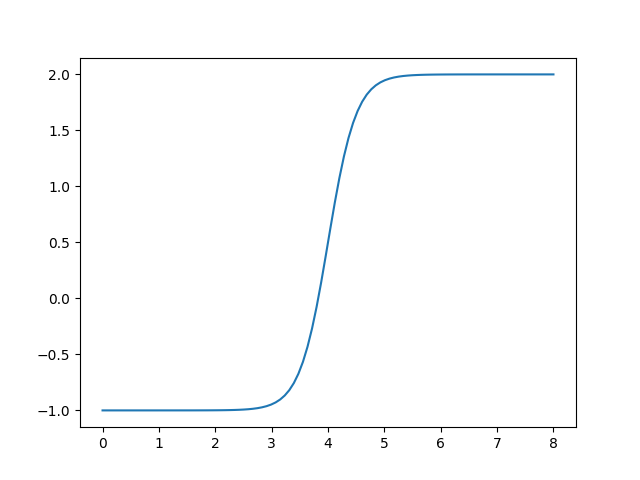
>>> from hydpy import ANN, nan
>>> ann = ANN(nmb_inputs=1, nmb_neurons=(1,), nmb_outputs=1,
...           weights_input=4.0, weights_output=3.0,
...           intercepts_hidden=-16.0, intercepts_output=-1.0)

The following loop subsequently sets the values 0 to 8 as input values, performs the calculation, and prints out the final output. As to be expected, the results show the shape of the logistic function:

>>> from hydpy import round_
>>> for input_ in range(9):
...     ann.inputs[0] = input_
...     ann.calculate_values()
...     round_([input_, ann.outputs[0]])
0, -1.0
1, -0.999982
2, -0.998994
3, -0.946041
4, 0.5
5, 1.946041
6, 1.998994
7, 1.999982
8, 2.0

One can also directly plot the resulting graph:

>>> figure = ann.plot(0.0, 8.0)

You can use the pyplot API of matplotlib to modify the figure or to save it to disk (or print it to the screen, in case the interactive mode of matplotlib is disabled):

>>> from hydpy.core.testtools import save_autofig
>>> save_autofig("ANN_plot.png", figure=figure)

Some models might require the derivative of certain outputs with respect to individual inputs. One example is application model the dam_llake, which uses class ANN to model the relationship between water storage and stage of a lake. During a simulation run , it additionally needs to know the area of the water surface, which is the derivative of storage with respect to stage. For such purposes, class ANN provides method calculate_derivatives(). In the following example, we apply this method and compare its results with finite difference approximations:

>>> d_input = 1e-8
>>> for input_ in range(9):
...     ann.inputs[0] = input_-d_input/2.0
...     ann.calculate_values()
...     value0 = ann.outputs[0]
...     ann.inputs[0] = input_+d_input/2.0
...     ann.calculate_values()
...     value1 = ann.outputs[0]
...     derivative = (value1-value0)/d_input
...     ann.inputs[0] = input_
...     ann.calculate_values()
...     ann.calculate_derivatives(0)
...     round_([input_, derivative, ann.output_derivatives[0]])
0, 0.000001, 0.000001
1, 0.000074, 0.000074
2, 0.004023, 0.004023
3, 0.211952, 0.211952
4, 3.0, 3.0
5, 0.211952, 0.211952
6, 0.004023, 0.004023
7, 0.000074, 0.000074
8, 0.000001, 0.000001

Note the following two potential pitfalls (both due to speeding up method calculate_derivatives()). First, for networks with more than one hidden layer, you must call calculate_values() before calling calculate_derivatives(). Second, method calculate_derivatives() calculates the derivatives with respect to a single input only, selected by the idx_input argument. However, it works fine to call method calculate_values() and then calculate_derivatives() multiple times afterwards. Thereby, you can subsequently pass different index values to calculate the derivatives with respect to different inputs.

The following example shows that everything works well for more complex single layer networks (we checked the results manually):

>>> ann.nmb_inputs = 3
>>> ann.nmb_neurons = (4,)
>>> ann.nmb_outputs = 2
>>> ann.weights_input = [[ 0.2, -0.1, -1.7,  0.6],
...                      [ 0.9,  0.2,  0.8,  0.0],
...                      [-0.5, -1.0,  2.3, -0.4]]
>>> ann.weights_output = [[ 0.0,  2.0],
...                       [-0.5,  1.0],
...                       [ 0.4,  2.4],
...                       [ 0.8, -0.9]]
>>> ann.intercepts_hidden = [ 0.9,  0.0, -0.4, -0.2]
>>> ann.intercepts_output = [ 1.3, -2.0]
>>> ann.inputs = [-0.1,  1.3,  1.6]
>>> ann.calculate_values()
>>> round_(ann.outputs)
1.822222, 1.876983

We again validate the calculated derivatives by comparison with numerical approximations:

>>> for idx_input in range(3):
...     ann.calculate_derivatives(idx_input)
...     round_(ann.output_derivatives)
0.099449, -0.103039
-0.01303, 0.365739
0.027041, -0.203965

>>> d_input = 1e-8
>>> for idx_input in range(3):
...     input_ = ann.inputs[idx_input]
...     ann.inputs[idx_input] = input_-d_input/2.0
...     ann.calculate_values()
...     values0 = ann.outputs.copy()
...     ann.inputs[idx_input] = input_+d_input/2.0
...     ann.calculate_values()
...     values1 = ann.outputs.copy()
...     ann.inputs[idx_input] = input_
...     round_((values1-values0)/d_input)
0.099449, -0.103039
-0.01303, 0.365739
0.027041, -0.203965

The next example shows how to solve the XOR problem with a two-layer network. As usual, 1 stands for True and 0 stands for False.

We define a network with two inputs (I1 and I2), two neurons in mthe first hidden layer (H11 and H12), one neuron in the second hidden layer (H2), and a single output (O1):

>>> ann.nmb_inputs = 2
>>> ann.nmb_neurons = (2, 1)
>>> ann.nmb_outputs = 1

The value of O1 shall be identical with the activation of H2:

>>> ann.weights_output = 1.0
>>> ann.intercepts_output = 0.0

We set all intercepts of the hidden layer’s neurons to 750 and initialise unnecessary matrix entries with “nan”. So, an input of 500 or 1000 results in an activation state of approximately zero or one, respectively:

>>> ann.intercepts_hidden = [[-750.0, -750.0],
...                          [-750.0, nan]]

The weighting factor between both inputs and H11 is 1000. Hence, one True input is sufficient to activate H1. In contrast, the weighting factor between both inputs and H12 is 500. Hence, two True inputs are required to activate H12:

>>> ann.weights_input= [[1000.0, 500.0],
...                     [1000.0, 500.0]]

The weighting factor between H11 and H2 is 1000. Hence, in principle, H11 can activate H2. However, the weighting factor between H12 and H2 is -1000. Hence, H12 prevents H2 from becoming activated even when H11 is activated:

>>> ann.weights_hidden= [[[1000.0],
...                      [-1000.0]]]

To recapitulate, H11 determines if at least one input is True, H12 determines if both inputs are True, and H2 determines if precisely one input is True, which is the solution for the XOR-problem:

>>> ann
ANN(
    nmb_inputs=2,
    nmb_neurons=(2, 1),
    weights_input=[[1000.0, 500.0],
                   [1000.0, 500.0]],
    weights_hidden=[[[1000.0],
                     [-1000.0]]],
    weights_output=[[1.0]],
    intercepts_hidden=[[-750.0, -750.0],
                       [-750.0, nan]],
    intercepts_output=[0.0],
)

The following calculation confirms the proper configuration of our network:

>>> for inputs in ((0.0, 0.0),
...                (1.0, 0.0),
...                (0.0, 1.0),
...                (1.0, 1.0)):
...    ann.inputs = inputs
...    ann.calculate_values()
...    round_([inputs[0], inputs[1], ann.outputs[0]])
0.0, 0.0, 0.0
1.0, 0.0, 1.0
0.0, 1.0, 1.0
1.0, 1.0, 0.0

To elaborate on the last calculation, we show the corresponding activations of the hidden neurons. As both inputs are True, both H12 (upper left value) and H22 (upper right value) are activated, but H2 (lower left value) is not:

>>> from hydpy import print_matrix
>>> print_matrix(ann.neurons)
| 1.0, 1.0 |
| 0.0, 0.0 |

Due to the sharp response function, the derivatives with respect to both inputs are approximately zero:

>>> for inputs in ((0.0, 0.0),
...                (1.0, 0.0),
...                (0.0, 1.0),
...                (1.0, 1.0)):
...    ann.inputs = inputs
...    ann.calculate_values()
...    ann.calculate_derivatives(0)
...    round_([inputs[0], inputs[1], ann.output_derivatives[0]])
0.0, 0.0, 0.0
1.0, 0.0, 0.0
0.0, 1.0, 0.0
1.0, 1.0, 0.0

To better validate the calculation of derivatives for multi-layer networks, we decrease our network’s weights (and, accordingly, the intercepts), making its response more smooth:

>>> ann = ANN(nmb_inputs=2,
...           nmb_neurons=(2, 1),
...           nmb_outputs=1,
...           weights_input=[[10.0, 5.0],
...                          [10.0, 5.0]],
...           weights_hidden=[[[10.0],
...                            [-10.0]]],
...           weights_output=[[1.0]],
...           intercepts_hidden=[[-7.5, -7.5],
...                              [-7.5, nan]],
...           intercepts_output=[0.0])

The results of method calculate_derivatives() again agree with those of the finite difference approximation:

>>> for inputs in ((0.0, 0.0),
...                (1.0, 0.0),
...                (0.0, 1.0),
...                (1.0, 1.0)):
...     ann.inputs = inputs
...     ann.calculate_values()
...     ann.calculate_derivatives(0)
...     derivative1 = ann.output_derivatives[0]
...     ann.calculate_derivatives(1)
...     derivative2 = ann.output_derivatives[0]
...     round_([inputs[0], inputs[1], derivative1, derivative2])
0.0, 0.0, 0.000015, 0.000015
1.0, 0.0, 0.694609, 0.694609
0.0, 1.0, 0.694609, 0.694609
1.0, 1.0, -0.004129, -0.004129

>>> d_input = 1e-8
>>> for inputs in ((0.0, 0.0),
...                (1.0, 0.0),
...                (0.0, 1.0),
...                (1.0, 1.0)):
...     derivatives = []
...     for idx_input in range(2):
...         ann.inputs = inputs
...         ann.inputs[idx_input] = inputs[idx_input]-d_input/2.0
...         ann.calculate_values()
...         value0 = ann.outputs[0]
...         ann.inputs[idx_input] = inputs[idx_input]+d_input/2.0
...         ann.calculate_values()
...         value1 = ann.outputs[0]
...         derivatives.append((value1-value0)/d_input)
...     round_([inputs[0], inputs[1]] + derivatives)
0.0, 0.0, 0.000015, 0.000015
1.0, 0.0, 0.694609, 0.694609
0.0, 1.0, 0.694609, 0.694609
1.0, 1.0, -0.004129, -0.004129

Note that Python class ANN handles a corresponding Cython extension class defined in annutils, which does not protect itself against segmentation faults. But class ANN takes up this task, meaning using its public members should always result in readable exceptions instead of program crashes, e.g.:

>>> corrupted = ANN()
>>> del corrupted.nmb_outputs
>>> corrupted.nmb_outputs
Traceback (most recent call last):
...
hydpy.core.exceptiontools.AttributeNotReady: Attribute `nmb_outputs` of object `ann` has not been prepared so far.

>>> corrupted.outputs
Traceback (most recent call last):
...
hydpy.core.exceptiontools.AttributeNotReady: Attribute `outputs` of object `ann` is not usable so far.  At least, you have to prepare attribute `nmb_outputs` first.

You can compare ANN objects for equality. The following exhaustive tests ensure that one ANN is only considered equal with another ANN object with the same network shape and parameter values:

>>> ann == ann
True

>>> ann == 1
False

>>> ann2 = ANN()
>>> ann2(nmb_inputs=2,
...      nmb_neurons=(2, 1),
...      nmb_outputs=1,
...      weights_input=[[10.0, 5.0],
...                     [10.0, 5.0]],
...      weights_hidden=[[[10.0],
...                       [-10.0]]],
...      weights_output=[[1.0]],
...      intercepts_hidden=[[-7.5, -7.5],
...                         [-7.5, nan]],
...      intercepts_output=[0.0])
>>> ann == ann2
True

>>> ann2.weights_input[0, 0] = nan
>>> ann == ann2
False
>>> ann2.weights_input[0, 0] = 10.0
>>> ann == ann2
True

>>> ann2.weights_hidden[0, 1, 0] = 5.0
>>> ann == ann2
False
>>> ann2.weights_hidden[0, 1, 0] = -10.0
>>> ann == ann2
True

>>> ann2.weights_output[0, 0] = 2.0
>>> ann == ann2
False
>>> ann2.weights_output[0, 0] = 1.0
>>> ann == ann2
True

>>> ann2.intercepts_hidden[1, 0] = nan
>>> ann == ann2
False
>>> ann2.intercepts_hidden[1, 0] = -7.5
>>> ann == ann2
True

>>> ann2.intercepts_output[0] = 0.1
>>> ann == ann2
False
>>> ann2.intercepts_output[0] = 0.0
>>> ann == ann2
True

>>> ann2.activation[0, 0] = 0
>>> ann == ann2
False
>>> ann2.activation[0, 0] = 1
>>> ann == ann2
True

>>> ann2(nmb_inputs=1,
...      nmb_neurons=(2, 1),
...      nmb_outputs=1)
>>> ann == ann2
False

>>> ann2(nmb_inputs=2,
...      nmb_neurons=(1, 1),
...      nmb_outputs=1)
>>> ann == ann2
False

>>> ann2(nmb_inputs=2,
...      nmb_neurons=(2, 1),
...      nmb_outputs=2)
>>> ann == ann2
False

nmb_inputs: BaseProperty[Never, int]¶: The number of input values.

nmb_outputs: BaseProperty[Never, int]¶: The lastly calculated output values.

nmb_neurons¶

The number of neurons of the hidden layers.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=3)
>>> ann.nmb_neurons
(2, 1)
>>> ann.nmb_neurons = (3,)
>>> ann.nmb_neurons
(3,)
>>> del ann.nmb_neurons
>>> ann.nmb_neurons
Traceback (most recent call last):
...
hydpy.core.exceptiontools.AttributeNotReady: Attribute `nmb_neurons` of object `ann` has not been prepared so far.

property nmb_weights_input: int¶

The number of input weights.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=3, nmb_neurons=(2, 1), nmb_outputs=1)
>>> ann.nmb_weights_input
6

property shape_weights_input: tuple[int, int]¶

The shape of the array containing the input weights.

The first integer value is the number of input nodes; the second integer value is the number of neurons of the first hidden layer:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=3, nmb_neurons=(2, 1), nmb_outputs=1)
>>> ann.shape_weights_input
(3, 2)

weights_input¶

The weights between all input nodes and neurons of the first hidden layer.

All “weight properties” of class ANN are usable as explained in-depth for the input weights below.

The input nodes and the neurons vary on the first and second axes of the: 2-dimensional array, respectively (see property shape_weights_input):

>>> from hydpy import ANN, print_matrix
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(3,))
>>> print_matrix(ann.weights_input)
| 0.0, 0.0, 0.0 |
| 0.0, 0.0, 0.0 |

The following error occurs when either the number of input nodes or of hidden neurons is unknown:

>>> del ann.nmb_inputs
>>> ann.weights_input
Traceback (most recent call last):
...
hydpy.core.exceptiontools.AttributeNotReady: Attribute `weights_input` of object `ann` is not usable so far.  At least, you have to prepare attribute `nmb_inputs` first.
>>> ann.nmb_inputs = 2

It is allowed to set values via slicing:

>>> ann.weights_input[:, 0] = 1.
>>> print_matrix(ann.weights_input)
| 1.0, 0.0, 0.0 |
| 1.0, 0.0, 0.0 |

If possible, property weights_input performs type conversions:

>>> ann.weights_input = "2"
>>> print_matrix(ann.weights_input)
| 2.0, 2.0, 2.0 |
| 2.0, 2.0, 2.0 |

One can assign whole matrices directly:

>>> import numpy
>>> ann.weights_input = numpy.eye(2, 3)
>>> print_matrix(ann.weights_input)
| 1.0, 0.0, 0.0 |
| 0.0, 1.0, 0.0 |

One can also delete the values contained in the array:

>>> del ann.weights_input
>>> print_matrix(ann.weights_input)
| 0.0, 0.0, 0.0 |
| 0.0, 0.0, 0.0 |

Errors like wrong shapes (or unconvertible inputs) result in error messages:

>>> ann.weights_input = numpy.eye(3)
Traceback (most recent call last):
...
ValueError: While trying to set the input weights of the artificial neural network `ann` of element `?`, the following error occurred: could not broadcast input array from shape (3,3) into shape (2,3)

property shape_weights_output: tuple[int, int]¶

The shape of the array containing the output weights.

The first integer value is the number of neurons of the first hidden layer; the second integer value is the number of output nodes:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=3)
>>> ann.shape_weights_output
(1, 3)

property nmb_weights_output: int¶

The number of output weights.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 4), nmb_outputs=3)
>>> ann.nmb_weights_output
12

weights_output¶

The weights between all neurons of the last hidden layer and the output nodes.

See the documentation on properties shape_weights_output and weights_input for further information.

property shape_weights_hidden: tuple[int, int, int]¶

The shape of the array containing the activation of the hidden neurons.

The first integer value is the number of connections between the hidden layers. The second integer value is the maximum number of neurons of all hidden layers feeding information into another hidden layer (all except the last one). Finally, the third integer value is the maximum number of neurons of all hidden layers receiving information from another hidden layer (all except the first one):

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=6, nmb_neurons=(4, 3, 2), nmb_outputs=6)
>>> ann.shape_weights_hidden
(2, 4, 3)
>>> ann(nmb_inputs=6, nmb_neurons=(4,), nmb_outputs=6)
>>> ann.shape_weights_hidden
(0, 0, 0)

property nmb_weights_hidden: int¶

The number of hidden weights.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(4, 3, 2), nmb_outputs=3)
>>> ann.nmb_weights_hidden
18

weights_hidden¶

The weights between the neurons of the different hidden layers.

See the documentation on properties shape_weights_hidden and weights_input for further information.

property shape_intercepts_hidden: tuple[int, int]¶

The shape of the array containing the intercepts of neurons of the hidden layers.

The first integer value is the number of hidden layers; the second integer value is the maximum number of neurons of all hidden layers:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=6, nmb_neurons=(4, 3, 2), nmb_outputs=6)
>>> ann.shape_intercepts_hidden
(3, 4)

property nmb_intercepts_hidden: int¶: The number of input intercepts.

intercepts_hidden¶

The intercepts of all neurons of the hidden layers.

See the documentation on properties shape_intercepts_hidden and weights_input for further information.

property shape_intercepts_output: tuple[int]¶

The shape of the array containing the intercepts of neurons of the hidden layers.

The only integer value is the number of output nodes:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=3)
>>> ann.shape_intercepts_output
(3,)

property nmb_intercepts_output: int¶

The number of output intercepts.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=3)
>>> ann.nmb_intercepts_output
3

intercepts_output¶

The intercepts of all output nodes.

See the documentation on properties shape_intercepts_output and weights_input for further information.

property shape_activation: tuple[int, int]¶

The shape of the array defining the activation function for each neuron of the hidden layers.

The first integer value is the number of hidden layers; the second integer value is the maximum number of neurons of all hidden layers:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=6, nmb_neurons=(4, 3, 2), nmb_outputs=6)
>>> ann.shape_activation
(3, 4)

activation¶

Indices for selecting suitable activation functions for the neurons of the hidden layers.

By default, ANN uses the logistic function for calculating the activation of the neurons of the hidden layers and uses the identity function for the output nodes. However, property activation allows defining other activation functions for the hidden neurons individually. So far, one can select the identity function and a “filter version” of the logistic function as alternatives – others might follow.

Assume a neuron receives input \(i_1\) and \(i_2\) from two nodes of the input layer or its upstream hidden layer. We wheight these input values as usual:

\(x_1 = c + w_1 \cdot i_1 + w_2 \cdot i_2\)

When selecting the identity function through setting the index value “0”, the activation of the considered neuron is:

\(a_1 = x_1\)

Using the identity function is helpful for educational examples and for bypassing input through one layer without introducing nonlinearity.

When selecting the logistic function through setting the index value “1”, the activation of the considered neuron is:

\(a_1 = 1-\frac{1}{1+exp(x_1)}\)

The logistic function is a standard function for constructing neural networks. It allows to approximate any relationship within a specific range and accuracy, provided the neural network is large enough.

When selecting the “filter version” of the logistic function through setting the index value “2”, the activation of the considered neuron is:

\(a_1 = 1-\frac{1}{1+exp(x_1)} \cdot i_1\)

“Filter version” means that our neuron now filters the input of the single input node placed at the corresponding position of its layer. This activation function helps force the output of a neural network to be zero but never negative beyond a certain threshold.

Like the main documentation on class ANN, we now define a relatively complex network to show that the “normal” and the derivative calculations work. This time, we set the activation function explicitly. “1” stands for the logistic function, which we first use for all hidden neurons:

>>> from hydpy.auxs.anntools import ANN
>>> from hydpy import round_
>>> ann = ANN(nmb_inputs=2,
...           nmb_neurons=(2, 2),
...           nmb_outputs=2,
...           weights_input=[[0.2, -0.1],
...                          [-1.7, 0.6]],
...           weights_hidden=[[[-.5, 1.0],
...                            [0.4, 2.4]]],
...           weights_output=[[0.8, -0.9],
...                           [0.5, -0.4]],
...           intercepts_hidden=[[0.9, 0.0],
...                              [-0.4, -0.2]],
...           intercepts_output=[1.3, -2.0],
...           activation=[[1, 1],
...                       [1, 1]])    
>>> ann.inputs = -0.1,  1.3
>>> ann.calculate_values()
>>> round_(ann.outputs)
2.074427, -2.734692
>>> for idx_input in range(2):
...     ann.calculate_derivatives(idx_input)
...     round_(ann.output_derivatives)
-0.006199, 0.006571
0.039804, -0.044169

In the next example, we want to apply the identity function for the second neuron of the first hidden layer and the first neuron of the second hidden layer. Therefore, we pass its index value “0” to the corresponding activation entries:

>>> ann.activation = [[1, 0], [0, 1]]
>>> ann
ANN(
    nmb_inputs=2,
    nmb_neurons=(2, 2),
    nmb_outputs=2,
    weights_input=[[0.2, -0.1],
                   [-1.7, 0.6]],
    weights_hidden=[[[-0.5, 1.0],
                     [0.4, 2.4]]],
    weights_output=[[0.8, -0.9],
                    [0.5, -0.4]],
    intercepts_hidden=[[0.9, 0.0],
                       [-0.4, -0.2]],
    intercepts_output=[1.3, -2.0],
    activation=[[1, 0],
                [0, 1]],
)

The agreement between the analytical and the numerical derivatives gives us confidence everything works fine:

>>> ann.calculate_values()
>>> round_(ann.outputs)
1.584373, -2.178468
>>> for idx_input in range(2):
...     ann.calculate_derivatives(idx_input)
...     round_(ann.output_derivatives)
-0.056898, 0.060219
0.369807, -0.394801
>>> d_input = 1e-8
>>> for idx_input in range(2):
...     input_ = ann.inputs[idx_input]
...     ann.inputs[idx_input] = input_-d_input/2.0
...     ann.calculate_values()
...     values0 = ann.outputs.copy()
...     ann.inputs[idx_input] = input_+d_input/2.0
...     ann.calculate_values()
...     values1 = ann.outputs.copy()
...     ann.inputs[idx_input] = input_
...     round_((values1-values0)/d_input)
-0.056898, 0.060219
0.369807, -0.394801

Finally, we perform the same check for the “filter version” of the logistic function:

>>> ann.activation = [[1, 2], [2, 1]]
>>> ann.calculate_values()
>>> round_(ann.outputs)
1.825606, -2.445682
>>> for idx_input in range(2):
...     ann.calculate_derivatives(idx_input)
...     round_(ann.output_derivatives)
0.009532, -0.011236
-0.001715, 0.02872
>>> d_input = 1e-8
>>> for idx_input in range(2):
...     input_ = ann.inputs[idx_input]
...     ann.inputs[idx_input] = input_-d_input/2.0
...     ann.calculate_values()
...     values0 = ann.outputs.copy()
...     ann.inputs[idx_input] = input_+d_input/2.0
...     ann.calculate_values()
...     values1 = ann.outputs.copy()
...     ann.inputs[idx_input] = input_
...     round_((values1-values0)/d_input)
0.009532, -0.011236
-0.001715, 0.02872

property shape_inputs: tuple[int]¶

The shape of the array containing the input values.

The only integer value is the number of input nodes:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=5, nmb_neurons=(2, 1), nmb_outputs=2)
>>> ann.shape_inputs
(5,)

inputs: BaseProperty[Never, ndarray[Any, dtype[float64]]]¶: The current input values.

property shape_outputs: tuple[int]¶

The shape of the array containing the output values.

The only integer value is the number of output nodes:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=6)
>>> ann.shape_outputs
(6,)

outputs: BaseProperty[Never, ndarray[Any, dtype[float64]]]¶: The lastly calculated output values.

property shape_output_derivatives: tuple[int]¶

The shape of the array containing the output derivatives.

The only integer value is the number of output nodes:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=6)
>>> ann.shape_output_derivatives
(6,)

output_derivatives: BaseProperty[Never, ndarray[Any, dtype[float64]]]¶: The lastly calculated first-order derivatives.

nmb_layers¶

The number of hidden layers.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(2, 1), nmb_outputs=3)
>>> ann.nmb_layers
2

shape_neurons¶

The shape of the array containing the activations of the neurons of the hidden layers.

The first integer value is the number of hidden layers; the second integer value is the maximum number of neurons of all hidden layers:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(4, 3, 2), nmb_outputs=6)
>>> ann.shape_neurons
(3, 4)

neurons¶

The activation of the neurons of the hidden layers.

See the documentation on properties shape_neurons and weights_input for further information.

shape_neuron_derivatives¶

The shape of the array containing the derivatives of the activities of the neurons of the hidden layers.

The first integer value is the number of hidden layers; the second integer value is the maximum number of neurons of all hidden layers:

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=2, nmb_neurons=(4, 3, 2), nmb_outputs=6)
>>> ann.shape_neuron_derivatives
(3, 4)

neuron_derivatives¶

The derivatives of the activation of the neurons of the hidden layers.

See the documentation on properties shape_neuron_derivatives and weights_input for further information.

calculate_values() → None[source]¶

Calculate the network output values based on the input values defined previously.

For more information, see the documentation on class ANN.

calculate_derivatives(idx: int, /) → None[source]¶

Calculate the derivatives of the network output values with respect to the input value of the given index.

For more information, see the documentation on class ANN.

property nmb_weights: int¶

The number of all input, inner, and output weights.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=1, nmb_neurons=(2, 3), nmb_outputs=4)
>>> ann.nmb_weights
20

property nmb_intercepts: int¶

The number of all inner and output intercepts.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=1, nmb_neurons=(2, 3), nmb_outputs=4)
>>> ann.nmb_intercepts
9

property nmb_parameters: int¶

The sum of nmb_weights and nmb_intercepts.

>>> from hydpy import ANN
>>> ann = ANN(nmb_inputs=1, nmb_neurons=(2, 3), nmb_outputs=4)
>>> ann.nmb_parameters
29

verify() → None[source]¶

Raise a RuntimeError if the network’s shape is not defined completely.

>>> from hydpy import ANN
>>> ann = ANN()
>>> del ann.nmb_inputs
>>> ann.verify()
Traceback (most recent call last):
...
RuntimeError: The shape of the the artificial neural network parameter `ann` of element `?` is not properly defined.

assignrepr(prefix: str, indent: int = 0) → str[source]¶: Return a string representation of the actual ANN object prefixed with the given string.

Table of Contents

Previous topic

Next topic

This Page

Versions

anntools¶