dam_v001¶
Version 1 application model of HydPy-Dam.
dam_v001 is supposed to represent a dam with an active low water
control scheme and a passive high water control scheme.
During low flow conditions, dam_v001 tries to increase low runoff
values immediately downstream the dam and at a more remote location
in the river channel downstream. This requires that dam_v001 receives
information from downstream via a receiver node. In order to achieve
a reliable drought control, dam_v001 to store some low-flow related
information for a certain number of simulation steps.
During high flow conditions, dam_v001 is controlled by two fixed
relationships: one between water volume and water level, the other
one between discharge and water level.
The differential equation of dam_v001 is solved by an adaptive
Runge-Kutta solver that only works well on continuous equations.
This is one reason why most threshold based low-flow equations are
defined in a smoothed manner, and why an artificial neural network
is chosen to specify the relationship between discharge and waterlevel.
(Additionally, the smoothed equations allow for a finer, less abrupt
control of the dam.) However, the proper (meaning realistic and
computational efficient) setting of the related smoothing and neural
network parameters might require some experience. It seems advisable
to investigate the functioning of each new model parameterization on
a number of synthetic and/or measured drought events.
Note also that the applied solver is an explicite Runge-Kutta method, which could increase computation times under stiffness. Due to to the adaptive order and stepsize control, inaccurate results due to stability issues should be excluded. But for very responsive dams increased computations times are to be expected. This is explained in some detail at the end of this section.
Integration tests¶
Note
When new to HydPy, consider reading section How to understand integration tests? first.
The following examples are performed over a period of 20 days:
>>> from hydpy import pub >>> pub.timegrids = "01.01.2000", "21.01.2000", "1d"The first examples are supposed to demonstrate how drought events at a cross section far downstream are reduced by the corresponding methods of the dam model under different configurations. To show this in a realistic manner, a relatively complex setting is required. We will make use of the
arma_v1application model. This model will be used to route the outflow of the dam to the cross section under investigation and add some natural discharge of the subcatchment between the dam and the cross section (a picture would be helpful).We define four nodes. The input_ node is used to define the inflow into the dam and the natural node is used to define the additional discharge of the subcatchment. The output node receives the (unmodified) outflow out of dam and the remote node receives both the routed outflow of the dam and the additional discharge of the subcatchment:
>>> from hydpy import Node >>> input_ = Node("input_") >>> output = Node("output") >>> natural = Node("natural") >>> remote = Node("remote")These nodes are used to connect the following three elements. There is one element for handling the
dammodel and there are two elements for handling different stream models. The model of element stream1 is supposed to route the outflow of the dam model with significant delay and the model of element stream2 is supposed to directly pass the discharge of the subcatchment:>>> from hydpy import Element >>> dam = Element("dam", inlets=input_, outlets=output, receivers=remote) >>> stream1 = Element("stream1", inlets=output, outlets=remote) >>> stream2 = Element("stream2", inlets=natural, outlets=remote)Now the models can be prepared. We begin with the stream2 model. By setting the
Responsesparameter in the following manner we define a pure Moving Average model that neither results in translation nor retention processes:>>> from hydpy import prepare_model >>> from hydpy.models import arma_v1 >>> arma_model = prepare_model(arma_v1) >>> stream2.model = arma_model >>> arma_model.parameters.control.responses(((), (1.0,))) >>> arma_model.parameters.update()The second stream model is also configured as pure Moving Average model but with a time delay of 1.8 days:
>>> arma_model = prepare_model(arma_v1) >>> stream1.model = arma_model >>> arma_model.parameters.control.responses(((), (0.2, 0.4, 0.3, 0.1))) >>> arma_model.parameters.update() >>> arma_model.sequences.logs.login = 0.0Last but not least, the dam model is initialized and handed over to its the dam element (different sets of parameters will be defined in the examples below):
>>> from hydpy.models.dam_v001 import * >>> parameterstep("1d") >>> dam.model = modelTo execute the following examples conveniently, a test function object is prepared:
>>> from hydpy import IntegrationTest >>> IntegrationTest.plotting_options.activated = ( ... fluxes.inflow, fluxes.outflow) >>> test = IntegrationTest( ... dam, ... inits=((states.watervolume, 0.0), ... (logs.loggedtotalremotedischarge, 1.9), ... (logs.loggedoutflow, 0.0), ... (stream1.model.sequences.logs.login, 0.0))) >>> test.dateformat = "%d.%m."Next the drought event needs to be defined. The natural discharge of the subcatchment decreases constantly for 9 days, than stays at constant level of 1 m³/s for 4 days, and finally increases constantly again:
>>> natural.sequences.sim.series = [ ... 1.8, 1.7, 1.6, 1.5, 1.4, 1.3, 1.2, 1.1, 1.0, 1.0, ... 1.0, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8]The inflow into the dam is assumened to remain constant for the whole simulation period:
>>> input_.sequences.sim.series = 1.0Finally, we can set the parameter values of the dam model. For the sake of simplicity, the relationship between water level and volume is assumed to be linear, which we accomplish by selecting the identity function as the
activationfunction of theWaterVolume2WaterLevelparameter:>>> watervolume2waterlevel( ... weights_input=1.0, weights_output=0.25, ... intercepts_hidden=0.0, intercepts_output=0.0, ... activation=0) >>> # This plot confirms the linearity of the defined relationship: >>> watervolume2waterlevel.plot(0.0, 100.0) >>> from hydpy.core.testtools import save_autofig >>> save_autofig("dam_v001_watervolume2waterlevel.png")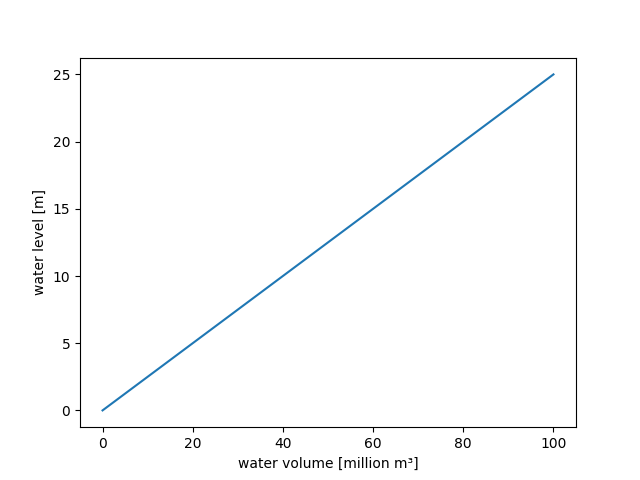
To focus on the drought related algorithms solely we turn of the flood related processes. This is accomplished by setting the weights and intercepts of the
WaterLevel2FloodDischargeto zero:>>> waterlevel2flooddischarge(ann( ... weights_input=0.0, weights_output=0.0, ... intercepts_hidden=0.0, intercepts_output=0.0)) >>> waterlevel2flooddischarge.plot(0.0, 25.0) >>> save_autofig("dam_v001_waterlevel2flooddischarge_1.png")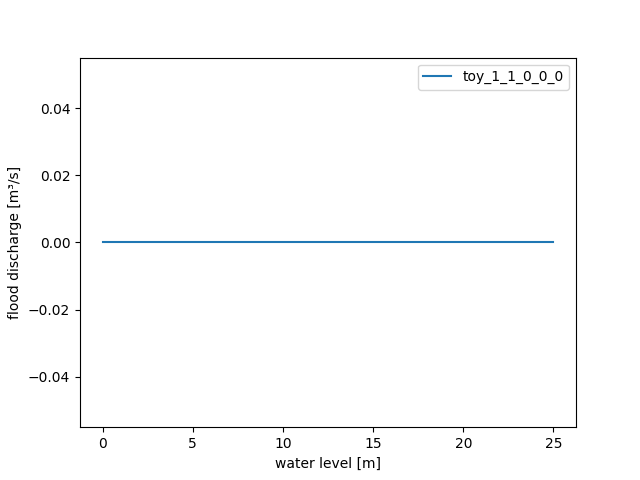
To confirm that the whole scenario is properly aranged, we also turn of of the drought related methods at first:
>>> nmblogentries(1) >>> remotedischargeminimum(0.0) >>> remotedischargesafety(0.0) >>> neardischargeminimumthreshold(0.0) >>> neardischargeminimumtolerance(0.0) >>> waterlevelminimumthreshold(0.0) >>> waterlevelminimumtolerance(0.0)Also, we have to define the area of the catchment draining into the dam. The information is required for adjusting the numerical local truncation error only. For a catchment area of 86.4 km² the general local truncation error (in mm per simulation step) is identical with the actually applied site specific local truncation error (in m³/s):
>>> catchmentarea(86.4) >>> from hydpy import round_ >>> round_(solver.abserrormax.INIT) 0.01 >>> parameters.update() >>> solver.abserrormax abserrormax(0.01)If not stated otherwise, we enable the
RestrictTargetedReleaseoption flag in the following examples:>>> restricttargetedrelease(True)Example 1
The following table confirms that the dam model does not release any discharge (row output contains zero values only). Hence the discharge at the cross section downstream (row remote) is identical with the discharge of the subcatchment (row natural):
Click here to see the graph>>> test("dam_v001_ex1") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ | 01.01. | 1.0 | 1.8 | 1.9 | 0.0 | -1.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0864 | 1.0 | 1.8 | 0.0 | 1.8 | | 02.01. | 1.0 | 1.7 | 1.8 | 0.0 | -1.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1728 | 1.0 | 1.7 | 0.0 | 1.7 | | 03.01. | 1.0 | 1.6 | 1.7 | 0.0 | -1.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2592 | 1.0 | 1.6 | 0.0 | 1.6 | | 04.01. | 1.0 | 1.5 | 1.6 | 0.0 | -1.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3456 | 1.0 | 1.5 | 0.0 | 1.5 | | 05.01. | 1.0 | 1.4 | 1.5 | 0.0 | -1.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.432 | 1.0 | 1.4 | 0.0 | 1.4 | | 06.01. | 1.0 | 1.3 | 1.4 | 0.0 | -1.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5184 | 1.0 | 1.3 | 0.0 | 1.3 | | 07.01. | 1.0 | 1.2 | 1.3 | 0.0 | -1.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.6048 | 1.0 | 1.2 | 0.0 | 1.2 | | 08.01. | 1.0 | 1.1 | 1.2 | 0.0 | -1.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.6912 | 1.0 | 1.1 | 0.0 | 1.1 | | 09.01. | 1.0 | 1.0 | 1.1 | 0.0 | -1.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.7776 | 1.0 | 1.0 | 0.0 | 1.0 | | 10.01. | 1.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.864 | 1.0 | 1.0 | 0.0 | 1.0 | | 11.01. | 1.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.9504 | 1.0 | 1.0 | 0.0 | 1.0 | | 12.01. | 1.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0368 | 1.0 | 1.0 | 0.0 | 1.0 | | 13.01. | 1.0 | 1.1 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.1232 | 1.0 | 1.1 | 0.0 | 1.1 | | 14.01. | 1.0 | 1.2 | 1.1 | 0.0 | -1.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.2096 | 1.0 | 1.2 | 0.0 | 1.2 | | 15.01. | 1.0 | 1.3 | 1.2 | 0.0 | -1.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.296 | 1.0 | 1.3 | 0.0 | 1.3 | | 16.01. | 1.0 | 1.4 | 1.3 | 0.0 | -1.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3824 | 1.0 | 1.4 | 0.0 | 1.4 | | 17.01. | 1.0 | 1.5 | 1.4 | 0.0 | -1.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.4688 | 1.0 | 1.5 | 0.0 | 1.5 | | 18.01. | 1.0 | 1.6 | 1.5 | 0.0 | -1.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.5552 | 1.0 | 1.6 | 0.0 | 1.6 | | 19.01. | 1.0 | 1.7 | 1.6 | 0.0 | -1.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.6416 | 1.0 | 1.7 | 0.0 | 1.7 | | 20.01. | 1.0 | 1.8 | 1.7 | 0.0 | -1.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.728 | 1.0 | 1.8 | 0.0 | 1.8 |Example 2
Next the discharge that should not be undercut at the cross section downstream is set to 1.4 m³/s:
>>> remotedischargeminimum(1.4)The dam model decreases the drought but is not very successful in doing so. The lowest discharge at the cross section is increased from 1 m³/s to approximately 1.2 m³/s in the beginning of the event, which is still below the threshold value of 1.4 m³/s. Furthermore, in the second half of the event too much discharge is released. On January 12, the discharge at the cross section is increased from 1 m³/s to approximately 1.6 m³/s:
Click here to see the graph>>> test("dam_v001_ex2") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.8 | 1.9 | 0.0 | -0.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0864 | 1.0 | 1.8 | 0.0 | 1.8 | | 02.01. | 1.0 | 1.7 | 1.8 | 0.0 | -0.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1728 | 1.0 | 1.7 | 0.0 | 1.7 | | 03.01. | 1.0 | 1.6 | 1.7 | 0.0 | -0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2592 | 1.0 | 1.6 | 0.0 | 1.6 | | 04.01. | 1.0 | 1.5 | 1.6 | 0.0 | -0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3456 | 1.0 | 1.5 | 0.0 | 1.5 | | 05.01. | 1.0 | 1.4 | 1.5 | 0.0 | -0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.432 | 1.0 | 1.4 | 0.0 | 1.4 | | 06.01. | 1.0 | 1.3 | 1.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5184 | 1.0 | 1.3 | 0.0 | 1.3 | | 07.01. | 1.0 | 1.22 | 1.3 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.0 | 0.1 | 0.59616 | 1.0 | 1.2 | 0.1 | 1.22 | | 08.01. | 1.0 | 1.196 | 1.12 | 0.28 | 0.18 | 0.28 | 0.28 | 0.28 | 0.28 | 0.0 | 0.28 | 0.658368 | 1.0 | 1.1 | 0.28 | 1.196 | | 09.01. | 1.0 | 1.2388 | 0.916 | 0.484 | 0.204 | 0.484 | 0.484 | 0.484 | 0.484 | 0.0 | 0.484 | 0.70295 | 1.0 | 1.0 | 0.484 | 1.2388 | | 10.01. | 1.0 | 1.41664 | 0.7548 | 0.6452 | 0.1612 | 0.6452 | 0.6452 | 0.6452 | 0.6452 | 0.0 | 0.6452 | 0.733605 | 1.0 | 1.0 | 0.6452 | 1.41664 | | 11.01. | 1.0 | 1.556992 | 0.77144 | 0.62856 | -0.01664 | 0.62856 | 0.62856 | 0.62856 | 0.62856 | 0.0 | 0.62856 | 0.765698 | 1.0 | 1.0 | 0.62856 | 1.556992 | | 12.01. | 1.0 | 1.587698 | 0.928432 | 0.471568 | -0.156992 | 0.471568 | 0.471568 | 0.471568 | 0.471568 | 0.0 | 0.471568 | 0.811354 | 1.0 | 1.0 | 0.471568 | 1.587698 | | 13.01. | 1.0 | 1.598489 | 1.11613 | 0.28387 | -0.187698 | 0.28387 | 0.28387 | 0.28387 | 0.28387 | 0.0 | 0.28387 | 0.873228 | 1.0 | 1.1 | 0.28387 | 1.598489 | | 14.01. | 1.0 | 1.534951 | 1.314619 | 0.085381 | -0.198489 | 0.085381 | 0.085381 | 0.085381 | 0.085381 | 0.0 | 0.085381 | 0.952251 | 1.0 | 1.2 | 0.085381 | 1.534951 | | 15.01. | 1.0 | 1.46647 | 1.44957 | 0.0 | -0.134951 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.038651 | 1.0 | 1.3 | 0.0 | 1.46647 | | 16.01. | 1.0 | 1.454001 | 1.46647 | 0.0 | -0.06647 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.125051 | 1.0 | 1.4 | 0.0 | 1.454001 | | 17.01. | 1.0 | 1.508538 | 1.454001 | 0.0 | -0.054001 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.211451 | 1.0 | 1.5 | 0.0 | 1.508538 | | 18.01. | 1.0 | 1.6 | 1.508538 | 0.0 | -0.108538 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.297851 | 1.0 | 1.6 | 0.0 | 1.6 | | 19.01. | 1.0 | 1.7 | 1.6 | 0.0 | -0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.384251 | 1.0 | 1.7 | 0.0 | 1.7 | | 20.01. | 1.0 | 1.8 | 1.7 | 0.0 | -0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.470651 | 1.0 | 1.8 | 0.0 | 1.8 |Example 3
The qualified success in the example above is due to the time delay of the information flow from the cross section to the dam and, more importantly, due to the travel time of the discharge released. A simple strategy to increase reliability would be to set a higher value for parameter
RemoteDischargeMinimum, e.g.:>>> remotedischargeminimum(1.6)Now there is only a small violation of threshold value on January, 6:
Click here to see the graph>>> test("dam_v001_ex3") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.8 | 1.9 | 0.0 | -0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0864 | 1.0 | 1.8 | 0.0 | 1.8 | | 02.01. | 1.0 | 1.7 | 1.8 | 0.0 | -0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1728 | 1.0 | 1.7 | 0.0 | 1.7 | | 03.01. | 1.0 | 1.6 | 1.7 | 0.0 | -0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2592 | 1.0 | 1.6 | 0.0 | 1.6 | | 04.01. | 1.0 | 1.5 | 1.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3456 | 1.0 | 1.5 | 0.0 | 1.5 | | 05.01. | 1.0 | 1.42 | 1.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.0 | 0.1 | 0.42336 | 1.0 | 1.4 | 0.1 | 1.42 | | 06.01. | 1.0 | 1.396 | 1.32 | 0.28 | 0.18 | 0.28 | 0.28 | 0.28 | 0.28 | 0.0 | 0.28 | 0.485568 | 1.0 | 1.3 | 0.28 | 1.396 | | 07.01. | 1.0 | 1.4388 | 1.116 | 0.484 | 0.204 | 0.484 | 0.484 | 0.484 | 0.484 | 0.0 | 0.484 | 0.53015 | 1.0 | 1.2 | 0.484 | 1.4388 | | 08.01. | 1.0 | 1.51664 | 0.9548 | 0.6452 | 0.1612 | 0.6452 | 0.6452 | 0.6452 | 0.6452 | 0.0 | 0.6452 | 0.560805 | 1.0 | 1.1 | 0.6452 | 1.51664 | | 09.01. | 1.0 | 1.576992 | 0.87144 | 0.72856 | 0.08336 | 0.72856 | 0.72856 | 0.72856 | 0.72856 | 0.0 | 0.72856 | 0.584258 | 1.0 | 1.0 | 0.72856 | 1.576992 | | 10.01. | 1.0 | 1.683698 | 0.848432 | 0.751568 | 0.023008 | 0.751568 | 0.751568 | 0.751568 | 0.751568 | 0.0 | 0.751568 | 0.605722 | 1.0 | 1.0 | 0.751568 | 1.683698 | | 11.01. | 1.0 | 1.717289 | 0.93213 | 0.66787 | -0.083698 | 0.66787 | 0.66787 | 0.66787 | 0.66787 | 0.0 | 0.66787 | 0.634418 | 1.0 | 1.0 | 0.66787 | 1.717289 | | 12.01. | 1.0 | 1.675591 | 1.049419 | 0.550581 | -0.117289 | 0.550581 | 0.550581 | 0.550581 | 0.550581 | 0.0 | 0.550581 | 0.673248 | 1.0 | 1.0 | 0.550581 | 1.675591 | | 13.01. | 1.0 | 1.690748 | 1.12501 | 0.47499 | -0.075591 | 0.47499 | 0.47499 | 0.47499 | 0.47499 | 0.0 | 0.47499 | 0.718609 | 1.0 | 1.1 | 0.47499 | 1.690748 | | 14.01. | 1.0 | 1.698806 | 1.215758 | 0.384242 | -0.090748 | 0.384242 | 0.384242 | 0.384242 | 0.384242 | 0.0 | 0.384242 | 0.77181 | 1.0 | 1.2 | 0.384242 | 1.698806 | | 15.01. | 1.0 | 1.708339 | 1.314564 | 0.285436 | -0.098806 | 0.285436 | 0.285436 | 0.285436 | 0.285436 | 0.0 | 0.285436 | 0.833549 | 1.0 | 1.3 | 0.285436 | 1.708339 | | 16.01. | 1.0 | 1.712365 | 1.422903 | 0.177097 | -0.108339 | 0.177097 | 0.177097 | 0.177097 | 0.177097 | 0.0 | 0.177097 | 0.904647 | 1.0 | 1.4 | 0.177097 | 1.712365 | | 17.01. | 1.0 | 1.70784 | 1.535269 | 0.064731 | -0.112365 | 0.064731 | 0.064731 | 0.064731 | 0.064731 | 0.0 | 0.064731 | 0.985455 | 1.0 | 1.5 | 0.064731 | 1.70784 | | 18.01. | 1.0 | 1.707565 | 1.643109 | 0.0 | -0.10784 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.071855 | 1.0 | 1.6 | 0.0 | 1.707565 | | 19.01. | 1.0 | 1.737129 | 1.707565 | 0.0 | -0.107565 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.158255 | 1.0 | 1.7 | 0.0 | 1.737129 | | 20.01. | 1.0 | 1.806473 | 1.737129 | 0.0 | -0.137129 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.244655 | 1.0 | 1.8 | 0.0 | 1.806473 |Example 4
While is is possible to simply increase the value of parameter
RemoteDischargeMinimum, it is often advisable to use parameterRemoteDischargeSafetyinstead:>>> remotedischargeminimum(1.4) >>> remotedischargesafety(0.5)Under this configuration, the threshold value is exceeded at each simulation time step. Additionally, the final storage content of the dam is about 4 % higher than in the last example, meaning the available water has been used more efficiently:
Click here to see the graph>>> test("dam_v001_ex4") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.80075 | 1.9 | 0.0 | -0.5 | 0.005 | 0.005 | 0.005 | 0.00375 | 0.0 | 0.00375 | 0.086076 | 1.0 | 1.8 | 0.00375 | 1.80075 | | 02.01. | 1.0 | 1.703953 | 1.797 | 0.0 | -0.40075 | 0.012265 | 0.012265 | 0.012265 | 0.012265 | 0.0 | 0.012265 | 0.171416 | 1.0 | 1.7 | 0.012265 | 1.703953 | | 03.01. | 1.0 | 1.611799 | 1.691688 | 0.0 | -0.303953 | 0.028841 | 0.028841 | 0.028841 | 0.028841 | 0.0 | 0.028841 | 0.255324 | 1.0 | 1.6 | 0.028841 | 1.611799 | | 04.01. | 1.0 | 1.528085 | 1.582958 | 0.0 | -0.211799 | 0.062468 | 0.062468 | 0.062468 | 0.062468 | 0.0 | 0.062468 | 0.336327 | 1.0 | 1.5 | 0.062468 | 1.528085 | | 05.01. | 1.0 | 1.458423 | 1.465616 | 0.0 | -0.128085 | 0.117784 | 0.117784 | 0.117784 | 0.117784 | 0.0 | 0.117784 | 0.412551 | 1.0 | 1.4 | 0.117784 | 1.458423 | | 06.01. | 1.0 | 1.417501 | 1.340639 | 0.059361 | -0.058423 | 0.243813 | 0.243813 | 0.243813 | 0.243813 | 0.0 | 0.243813 | 0.477885 | 1.0 | 1.3 | 0.243813 | 1.417501 | | 07.01. | 1.0 | 1.430358 | 1.173688 | 0.226312 | -0.017501 | 0.456251 | 0.456251 | 0.456251 | 0.456251 | 0.0 | 0.456251 | 0.524865 | 1.0 | 1.2 | 0.456251 | 1.430358 | | 08.01. | 1.0 | 1.495671 | 0.974107 | 0.425893 | -0.030358 | 0.641243 | 0.641243 | 0.641243 | 0.641243 | 0.0 | 0.641243 | 0.555862 | 1.0 | 1.1 | 0.641243 | 1.495671 | | 09.01. | 1.0 | 1.556202 | 0.854428 | 0.545572 | -0.095671 | 0.692239 | 0.692239 | 0.692239 | 0.692239 | 0.0 | 0.692239 | 0.582452 | 1.0 | 1.0 | 0.692239 | 1.556202 | | 10.01. | 1.0 | 1.641325 | 0.863962 | 0.536038 | -0.156202 | 0.632157 | 0.632157 | 0.632157 | 0.632157 | 0.0 | 0.632157 | 0.614234 | 1.0 | 1.0 | 0.632157 | 1.641325 | | 11.01. | 1.0 | 1.612641 | 1.009168 | 0.390832 | -0.241325 | 0.439912 | 0.439912 | 0.439912 | 0.439912 | 0.0 | 0.439912 | 0.662625 | 1.0 | 1.0 | 0.439912 | 1.612641 | | 12.01. | 1.0 | 1.492699 | 1.172729 | 0.227271 | -0.212641 | 0.289317 | 0.289317 | 0.289317 | 0.289317 | 0.0 | 0.289317 | 0.724028 | 1.0 | 1.0 | 0.289317 | 1.492699 | | 13.01. | 1.0 | 1.480143 | 1.203382 | 0.196618 | -0.092699 | 0.346132 | 0.346132 | 0.346132 | 0.346132 | 0.0 | 0.346132 | 0.780523 | 1.0 | 1.1 | 0.346132 | 1.480143 | | 14.01. | 1.0 | 1.554814 | 1.13401 | 0.26599 | -0.080143 | 0.427871 | 0.427871 | 0.427871 | 0.427871 | 0.0 | 0.427871 | 0.829954 | 1.0 | 1.2 | 0.427871 | 1.554814 | | 15.01. | 1.0 | 1.677954 | 1.126942 | 0.273058 | -0.154814 | 0.370171 | 0.370171 | 0.370171 | 0.370171 | 0.0 | 0.370171 | 0.884372 | 1.0 | 1.3 | 0.370171 | 1.677954 | | 16.01. | 1.0 | 1.736699 | 1.307783 | 0.092217 | -0.277954 | 0.12828 | 0.12828 | 0.12828 | 0.12828 | 0.0 | 0.12828 | 0.959688 | 1.0 | 1.4 | 0.12828 | 1.736699 | | 17.01. | 1.0 | 1.709485 | 1.608419 | 0.0 | -0.336699 | 0.021671 | 0.021671 | 0.021671 | 0.021671 | 0.0 | 0.021671 | 1.044216 | 1.0 | 1.5 | 0.021671 | 1.709485 | | 18.01. | 1.0 | 1.689667 | 1.687814 | 0.0 | -0.309485 | 0.02749 | 0.02749 | 0.02749 | 0.02749 | 0.0 | 0.02749 | 1.128241 | 1.0 | 1.6 | 0.02749 | 1.689667 | | 19.01. | 1.0 | 1.73685 | 1.662178 | 0.0 | -0.289667 | 0.032623 | 0.032623 | 0.032623 | 0.032623 | 0.0 | 0.032623 | 1.211822 | 1.0 | 1.7 | 0.032623 | 1.73685 | | 20.01. | 1.0 | 1.827792 | 1.704227 | 0.0 | -0.33685 | 0.021642 | 0.021642 | 0.021642 | 0.021642 | 0.0 | 0.021642 | 1.296352 | 1.0 | 1.8 | 0.021642 | 1.827792 |Example 5
Building upon the last example, we subsequently increase the complexity of the model parameterization. Firstly, we introduce a required minimum water release of 0.2 m³/s:
>>> neardischargeminimumthreshold(0.2)Now there is also a relevant water release before and after the drought event occurs:
Click here to see the graph>>> test("dam_v001_ex5") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.838333 | 1.9 | 0.0 | -0.5 | 0.005 | 0.2 | 0.2 | 0.191667 | 0.0 | 0.191667 | 0.06984 | 1.0 | 1.8 | 0.191667 | 1.838333 | | 02.01. | 1.0 | 1.816667 | 1.646667 | 0.0 | -0.438333 | 0.008746 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.13896 | 1.0 | 1.7 | 0.2 | 1.816667 | | 03.01. | 1.0 | 1.7775 | 1.616667 | 0.0 | -0.416667 | 0.010632 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.20808 | 1.0 | 1.6 | 0.2 | 1.7775 | | 04.01. | 1.0 | 1.699167 | 1.5775 | 0.0 | -0.3775 | 0.015099 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2772 | 1.0 | 1.5 | 0.2 | 1.699167 | | 05.01. | 1.0 | 1.6 | 1.499167 | 0.0 | -0.299167 | 0.03006 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.34632 | 1.0 | 1.4 | 0.2 | 1.6 | | 06.01. | 1.0 | 1.5 | 1.4 | 0.0 | -0.2 | 0.068641 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.41544 | 1.0 | 1.3 | 0.2 | 1.5 | | 07.01. | 1.0 | 1.408516 | 1.3 | 0.1 | -0.1 | 0.242578 | 0.242578 | 0.242578 | 0.242578 | 0.0 | 0.242578 | 0.480881 | 1.0 | 1.2 | 0.242578 | 1.408516 | | 08.01. | 1.0 | 1.371888 | 1.165937 | 0.234063 | -0.008516 | 0.474285 | 0.474285 | 0.474285 | 0.474285 | 0.0 | 0.474285 | 0.526303 | 1.0 | 1.1 | 0.474285 | 1.371888 | | 09.01. | 1.0 | 1.43939 | 0.897603 | 0.502397 | 0.028112 | 0.784512 | 0.784512 | 0.784512 | 0.784512 | 0.0 | 0.784512 | 0.544921 | 1.0 | 1.0 | 0.784512 | 1.43939 | | 10.01. | 1.0 | 1.67042 | 0.654878 | 0.745122 | -0.03939 | 0.95036 | 0.95036 | 0.95036 | 0.95036 | 0.0 | 0.95036 | 0.54921 | 1.0 | 1.0 | 0.95036 | 1.67042 | | 11.01. | 1.0 | 1.806604 | 0.720061 | 0.679939 | -0.27042 | 0.71839 | 0.71839 | 0.71839 | 0.71839 | 0.0 | 0.71839 | 0.573541 | 1.0 | 1.0 | 0.71839 | 1.806604 | | 12.01. | 1.0 | 1.7156 | 1.088214 | 0.311786 | -0.406604 | 0.323424 | 0.323424 | 0.323424 | 0.323424 | 0.0 | 0.323424 | 0.631997 | 1.0 | 1.0 | 0.323424 | 1.7156 | | 13.01. | 1.0 | 1.579922 | 1.392176 | 0.007824 | -0.3156 | 0.03389 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.701117 | 1.0 | 1.1 | 0.2 | 1.579922 | | 14.01. | 1.0 | 1.488866 | 1.379922 | 0.020078 | -0.179922 | 0.100394 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.770237 | 1.0 | 1.2 | 0.2 | 1.488866 | | 15.01. | 1.0 | 1.525216 | 1.288866 | 0.111134 | -0.088866 | 0.264366 | 0.264366 | 0.264366 | 0.264366 | 0.0 | 0.264366 | 0.833796 | 1.0 | 1.3 | 0.264366 | 1.525216 | | 16.01. | 1.0 | 1.637612 | 1.260849 | 0.139151 | -0.125216 | 0.259326 | 0.259326 | 0.259326 | 0.259326 | 0.0 | 0.259326 | 0.89779 | 1.0 | 1.4 | 0.259326 | 1.637612 | | 17.01. | 1.0 | 1.74304 | 1.378286 | 0.021714 | -0.237612 | 0.072326 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.96691 | 1.0 | 1.5 | 0.2 | 1.74304 | | 18.01. | 1.0 | 1.824234 | 1.54304 | 0.0 | -0.34304 | 0.020494 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.03603 | 1.0 | 1.6 | 0.2 | 1.824234 | | 19.01. | 1.0 | 1.905933 | 1.624234 | 0.0 | -0.424234 | 0.009932 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.10515 | 1.0 | 1.7 | 0.2 | 1.905933 | | 20.01. | 1.0 | 2.0 | 1.705933 | 0.0 | -0.505933 | 0.004737 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.17427 | 1.0 | 1.8 | 0.2 | 2.0 |Example 6
One may have noted that the water release is only 0.19 m³/s instead of 0.2 m³/s on January 1. This is due to the low local truncation error of 1e-2 m³/s in combination with the fact that the simulation starts with an completely dry dam. To confirm this, the required numerical accuracy is increased temporarily:
>>> solver.abserrormax(1e-6)Now there is only a tiny deviation left in the last shown digit:
Click here to see the graph>>> test("dam_v001_ex6") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.84 | 1.9 | 0.0 | -0.5 | 0.005 | 0.2 | 0.2 | 0.199998 | 0.0 | 0.199998 | 0.06912 | 1.0 | 1.8 | 0.199998 | 1.84 | | 02.01. | 1.0 | 1.819999 | 1.640002 | 0.0 | -0.44 | 0.008615 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.13824 | 1.0 | 1.7 | 0.2 | 1.819999 | | 03.01. | 1.0 | 1.779999 | 1.619999 | 0.0 | -0.419999 | 0.010318 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.20736 | 1.0 | 1.6 | 0.2 | 1.779999 | | 04.01. | 1.0 | 1.7 | 1.579999 | 0.0 | -0.379999 | 0.014766 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.27648 | 1.0 | 1.5 | 0.2 | 1.7 | | 05.01. | 1.0 | 1.6 | 1.5 | 0.0 | -0.3 | 0.029844 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.3456 | 1.0 | 1.4 | 0.2 | 1.6 | | 06.01. | 1.0 | 1.5 | 1.4 | 0.0 | -0.2 | 0.068641 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.41472 | 1.0 | 1.3 | 0.2 | 1.5 | | 07.01. | 1.0 | 1.408516 | 1.3 | 0.1 | -0.1 | 0.242578 | 0.242578 | 0.242578 | 0.242578 | 0.0 | 0.242578 | 0.480161 | 1.0 | 1.2 | 0.242578 | 1.408516 | | 08.01. | 1.0 | 1.371888 | 1.165937 | 0.234063 | -0.008516 | 0.474285 | 0.474285 | 0.474285 | 0.474285 | 0.0 | 0.474285 | 0.525583 | 1.0 | 1.1 | 0.474285 | 1.371888 | | 09.01. | 1.0 | 1.43939 | 0.897603 | 0.502397 | 0.028112 | 0.784512 | 0.784512 | 0.784512 | 0.784512 | 0.0 | 0.784512 | 0.544201 | 1.0 | 1.0 | 0.784512 | 1.43939 | | 10.01. | 1.0 | 1.67042 | 0.654878 | 0.745122 | -0.03939 | 0.95036 | 0.95036 | 0.95036 | 0.95036 | 0.0 | 0.95036 | 0.54849 | 1.0 | 1.0 | 0.95036 | 1.67042 | | 11.01. | 1.0 | 1.806604 | 0.720061 | 0.679939 | -0.27042 | 0.71839 | 0.71839 | 0.71839 | 0.71839 | 0.0 | 0.71839 | 0.572821 | 1.0 | 1.0 | 0.71839 | 1.806604 | | 12.01. | 1.0 | 1.7156 | 1.088214 | 0.311786 | -0.406604 | 0.323424 | 0.323424 | 0.323424 | 0.323424 | 0.0 | 0.323424 | 0.631278 | 1.0 | 1.0 | 0.323424 | 1.7156 | | 13.01. | 1.0 | 1.579922 | 1.392176 | 0.007824 | -0.3156 | 0.03389 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.700398 | 1.0 | 1.1 | 0.2 | 1.579922 | | 14.01. | 1.0 | 1.488866 | 1.379922 | 0.020078 | -0.179922 | 0.100394 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.769518 | 1.0 | 1.2 | 0.2 | 1.488866 | | 15.01. | 1.0 | 1.525216 | 1.288866 | 0.111134 | -0.088866 | 0.264366 | 0.264366 | 0.264366 | 0.264366 | 0.0 | 0.264366 | 0.833076 | 1.0 | 1.3 | 0.264366 | 1.525216 | | 16.01. | 1.0 | 1.637612 | 1.260849 | 0.139151 | -0.125216 | 0.259326 | 0.259326 | 0.259326 | 0.259326 | 0.0 | 0.259326 | 0.897071 | 1.0 | 1.4 | 0.259326 | 1.637612 | | 17.01. | 1.0 | 1.74304 | 1.378286 | 0.021714 | -0.237612 | 0.072326 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.966191 | 1.0 | 1.5 | 0.2 | 1.74304 | | 18.01. | 1.0 | 1.824234 | 1.54304 | 0.0 | -0.34304 | 0.020494 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.035311 | 1.0 | 1.6 | 0.2 | 1.824234 | | 19.01. | 1.0 | 1.905933 | 1.624234 | 0.0 | -0.424234 | 0.009932 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.104431 | 1.0 | 1.7 | 0.2 | 1.905933 | | 20.01. | 1.0 | 2.0 | 1.705933 | 0.0 | -0.505933 | 0.004737 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.173551 | 1.0 | 1.8 | 0.2 | 2.0 |>>> solver.abserrormax(1e-2)Example 7
To allow for a smooth transition of the water release in periods where the highest demand switches from remote to near or the other way round, one can increase the value of the neardischargeminimumtolerance parameter:
>>> neardischargeminimumtolerance(0.2)It is easiest to inspect the functioning the effect of this “smooth switch” by looking at the results of column requiredrelease:
Click here to see the graph>>> test("dam_v001_ex7") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.840351 | 1.9 | 0.0 | -0.5 | 0.005 | 0.210526 | 0.210526 | 0.201754 | 0.0 | 0.201754 | 0.068968 | 1.0 | 1.8 | 0.201754 | 1.840351 | | 02.01. | 1.0 | 1.822886 | 1.638597 | 0.0 | -0.440351 | 0.008588 | 0.21092 | 0.21092 | 0.21092 | 0.0 | 0.21092 | 0.137145 | 1.0 | 1.7 | 0.21092 | 1.822886 | | 03.01. | 1.0 | 1.787111 | 1.611966 | 0.0 | -0.422886 | 0.010053 | 0.211084 | 0.211084 | 0.211084 | 0.0 | 0.211084 | 0.205307 | 1.0 | 1.6 | 0.211084 | 1.787111 | | 04.01. | 1.0 | 1.71019 | 1.576027 | 0.0 | -0.387111 | 0.013858 | 0.211523 | 0.211523 | 0.211523 | 0.0 | 0.211523 | 0.273432 | 1.0 | 1.5 | 0.211523 | 1.71019 | | 05.01. | 1.0 | 1.611668 | 1.498667 | 0.0 | -0.31019 | 0.027322 | 0.213209 | 0.213209 | 0.213209 | 0.0 | 0.213209 | 0.34141 | 1.0 | 1.4 | 0.213209 | 1.611668 | | 06.01. | 1.0 | 1.513658 | 1.398459 | 0.001541 | -0.211668 | 0.064075 | 0.219043 | 0.219043 | 0.219043 | 0.0 | 0.219043 | 0.408885 | 1.0 | 1.3 | 0.219043 | 1.513658 | | 07.01. | 1.0 | 1.429416 | 1.294615 | 0.105385 | -0.113658 | 0.235523 | 0.283419 | 0.283419 | 0.283419 | 0.0 | 0.283419 | 0.470798 | 1.0 | 1.2 | 0.283419 | 1.429416 | | 08.01. | 1.0 | 1.395444 | 1.145997 | 0.254003 | -0.029416 | 0.470414 | 0.475212 | 0.475212 | 0.475212 | 0.0 | 0.475212 | 0.516139 | 1.0 | 1.1 | 0.475212 | 1.395444 | | 09.01. | 1.0 | 1.444071 | 0.920232 | 0.479768 | 0.004556 | 0.735001 | 0.735281 | 0.735281 | 0.735281 | 0.0 | 0.735281 | 0.539011 | 1.0 | 1.0 | 0.735281 | 1.444071 | | 10.01. | 1.0 | 1.643281 | 0.70879 | 0.69121 | -0.044071 | 0.891263 | 0.891315 | 0.891315 | 0.891315 | 0.0 | 0.891315 | 0.548402 | 1.0 | 1.0 | 0.891315 | 1.643281 | | 11.01. | 1.0 | 1.763981 | 0.751966 | 0.648034 | -0.243281 | 0.696325 | 0.696749 | 0.696749 | 0.696749 | 0.0 | 0.696749 | 0.574602 | 1.0 | 1.0 | 0.696749 | 1.763981 | | 12.01. | 1.0 | 1.692903 | 1.067232 | 0.332768 | -0.363981 | 0.349797 | 0.366406 | 0.366406 | 0.366406 | 0.0 | 0.366406 | 0.629345 | 1.0 | 1.0 | 0.366406 | 1.692903 | | 13.01. | 1.0 | 1.590367 | 1.326497 | 0.073503 | -0.292903 | 0.105231 | 0.228241 | 0.228241 | 0.228241 | 0.0 | 0.228241 | 0.696025 | 1.0 | 1.1 | 0.228241 | 1.590367 | | 14.01. | 1.0 | 1.516904 | 1.362126 | 0.037874 | -0.190367 | 0.111928 | 0.230054 | 0.230054 | 0.230054 | 0.0 | 0.230054 | 0.762548 | 1.0 | 1.2 | 0.230054 | 1.516904 | | 15.01. | 1.0 | 1.554409 | 1.28685 | 0.11315 | -0.116904 | 0.240436 | 0.286374 | 0.286374 | 0.286374 | 0.0 | 0.286374 | 0.824205 | 1.0 | 1.3 | 0.286374 | 1.554409 | | 16.01. | 1.0 | 1.662351 | 1.268035 | 0.131965 | -0.154409 | 0.229369 | 0.279807 | 0.279807 | 0.279807 | 0.0 | 0.279807 | 0.88643 | 1.0 | 1.4 | 0.279807 | 1.662351 | | 17.01. | 1.0 | 1.764451 | 1.382544 | 0.017456 | -0.262351 | 0.058622 | 0.21805 | 0.21805 | 0.21805 | 0.0 | 0.21805 | 0.953991 | 1.0 | 1.5 | 0.21805 | 1.764451 | | 18.01. | 1.0 | 1.842178 | 1.5464 | 0.0 | -0.364451 | 0.016958 | 0.211892 | 0.211892 | 0.211892 | 0.0 | 0.211892 | 1.022083 | 1.0 | 1.6 | 0.211892 | 1.842178 | | 19.01. | 1.0 | 1.920334 | 1.630286 | 0.0 | -0.442178 | 0.008447 | 0.210904 | 0.210904 | 0.210904 | 0.0 | 0.210904 | 1.090261 | 1.0 | 1.7 | 0.210904 | 1.920334 | | 20.01. | 1.0 | 2.011822 | 1.709429 | 0.0 | -0.520334 | 0.004155 | 0.210435 | 0.210435 | 0.210435 | 0.0 | 0.210435 | 1.158479 | 1.0 | 1.8 | 0.210435 | 2.011822 |Example 8.1
dam_v001is forced to keep a certain degree of low flow variability when the option flagRestrictTargetedReleaseis enabled. Then it is not allowed to release an arbitrary amount of water when the inflow falls below the required minimum water release. We show this by decreasing the inflow in the second half of the simulation period to 0.1 m³/s:>>> input_.sequences.sim.series[10:] = 0.1The value of parameter
NearDischargeMinimumThreshold(0.2 m³/s) is maintained, but the value ofNearDischargeMinimumToleranceis reset to 0 m³/s for improving comprehensibility:>>> neardischargeminimumtolerance(0.0)As to be expected, the actual release drops to 0.1 m³/s on January 11. But, due to the time delay of the discharge released earlier, the largest violation of the threshold value takes place on January, 13:
Click here to see the graph>>> test("dam_v001_ex8_1") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.838333 | 1.9 | 0.0 | -0.5 | 0.005 | 0.2 | 0.2 | 0.191667 | 0.0 | 0.191667 | 0.06984 | 1.0 | 1.8 | 0.191667 | 1.838333 | | 02.01. | 1.0 | 1.816667 | 1.646667 | 0.0 | -0.438333 | 0.008746 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.13896 | 1.0 | 1.7 | 0.2 | 1.816667 | | 03.01. | 1.0 | 1.7775 | 1.616667 | 0.0 | -0.416667 | 0.010632 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.20808 | 1.0 | 1.6 | 0.2 | 1.7775 | | 04.01. | 1.0 | 1.699167 | 1.5775 | 0.0 | -0.3775 | 0.015099 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2772 | 1.0 | 1.5 | 0.2 | 1.699167 | | 05.01. | 1.0 | 1.6 | 1.499167 | 0.0 | -0.299167 | 0.03006 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.34632 | 1.0 | 1.4 | 0.2 | 1.6 | | 06.01. | 1.0 | 1.5 | 1.4 | 0.0 | -0.2 | 0.068641 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.41544 | 1.0 | 1.3 | 0.2 | 1.5 | | 07.01. | 1.0 | 1.408516 | 1.3 | 0.1 | -0.1 | 0.242578 | 0.242578 | 0.242578 | 0.242578 | 0.0 | 0.242578 | 0.480881 | 1.0 | 1.2 | 0.242578 | 1.408516 | | 08.01. | 1.0 | 1.371888 | 1.165937 | 0.234063 | -0.008516 | 0.474285 | 0.474285 | 0.474285 | 0.474285 | 0.0 | 0.474285 | 0.526303 | 1.0 | 1.1 | 0.474285 | 1.371888 | | 09.01. | 1.0 | 1.43939 | 0.897603 | 0.502397 | 0.028112 | 0.784512 | 0.784512 | 0.784512 | 0.784512 | 0.0 | 0.784512 | 0.544921 | 1.0 | 1.0 | 0.784512 | 1.43939 | | 10.01. | 1.0 | 1.67042 | 0.654878 | 0.745122 | -0.03939 | 0.95036 | 0.95036 | 0.95036 | 0.95036 | 0.0 | 0.95036 | 0.54921 | 1.0 | 1.0 | 0.95036 | 1.67042 | | 11.01. | 0.1 | 1.682926 | 0.720061 | 0.679939 | -0.27042 | 0.71839 | 0.71839 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.0 | 0.1 | 1.682926 | | 12.01. | 0.1 | 1.423559 | 1.582926 | 0.0 | -0.282926 | 0.034564 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.0 | 0.1 | 1.423559 | | 13.01. | 0.1 | 1.285036 | 1.323559 | 0.076441 | -0.023559 | 0.299482 | 0.299482 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.1 | 0.1 | 1.285036 | | 14.01. | 0.1 | 1.3 | 1.185036 | 0.214964 | 0.114964 | 0.585979 | 0.585979 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.2 | 0.1 | 1.3 | | 15.01. | 0.1 | 1.4 | 1.2 | 0.2 | 0.1 | 0.557422 | 0.557422 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.3 | 0.1 | 1.4 | | 16.01. | 0.1 | 1.5 | 1.3 | 0.1 | 0.0 | 0.35 | 0.35 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.4 | 0.1 | 1.5 | | 17.01. | 0.1 | 1.6 | 1.4 | 0.0 | -0.1 | 0.142578 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.5 | 0.1 | 1.6 | | 18.01. | 0.1 | 1.7 | 1.5 | 0.0 | -0.2 | 0.068641 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.6 | 0.1 | 1.7 | | 19.01. | 0.1 | 1.8 | 1.6 | 0.0 | -0.3 | 0.029844 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.7 | 0.1 | 1.8 | | 20.01. | 0.1 | 1.9 | 1.7 | 0.0 | -0.4 | 0.012348 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.54921 | 0.1 | 1.8 | 0.1 | 1.9 |Example 8.2
This modification of the last example shows that with an disabled
RestrictTargetedReleaseflag the amount of water released is allowed to exceed the the inflow in any case:Click here to see the graph>>> restricttargetedrelease(False) >>> test("dam_v001_ex8_2") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.838333 | 1.9 | 0.0 | -0.5 | 0.005 | 0.2 | 0.2 | 0.191667 | 0.0 | 0.191667 | 0.06984 | 1.0 | 1.8 | 0.191667 | 1.838333 | | 02.01. | 1.0 | 1.816667 | 1.646667 | 0.0 | -0.438333 | 0.008746 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.13896 | 1.0 | 1.7 | 0.2 | 1.816667 | | 03.01. | 1.0 | 1.7775 | 1.616667 | 0.0 | -0.416667 | 0.010632 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.20808 | 1.0 | 1.6 | 0.2 | 1.7775 | | 04.01. | 1.0 | 1.699167 | 1.5775 | 0.0 | -0.3775 | 0.015099 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2772 | 1.0 | 1.5 | 0.2 | 1.699167 | | 05.01. | 1.0 | 1.6 | 1.499167 | 0.0 | -0.299167 | 0.03006 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.34632 | 1.0 | 1.4 | 0.2 | 1.6 | | 06.01. | 1.0 | 1.5 | 1.4 | 0.0 | -0.2 | 0.068641 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.41544 | 1.0 | 1.3 | 0.2 | 1.5 | | 07.01. | 1.0 | 1.408516 | 1.3 | 0.1 | -0.1 | 0.242578 | 0.242578 | 0.242578 | 0.242578 | 0.0 | 0.242578 | 0.480881 | 1.0 | 1.2 | 0.242578 | 1.408516 | | 08.01. | 1.0 | 1.371888 | 1.165937 | 0.234063 | -0.008516 | 0.474285 | 0.474285 | 0.474285 | 0.474285 | 0.0 | 0.474285 | 0.526303 | 1.0 | 1.1 | 0.474285 | 1.371888 | | 09.01. | 1.0 | 1.43939 | 0.897603 | 0.502397 | 0.028112 | 0.784512 | 0.784512 | 0.784512 | 0.784512 | 0.0 | 0.784512 | 0.544921 | 1.0 | 1.0 | 0.784512 | 1.43939 | | 10.01. | 1.0 | 1.67042 | 0.654878 | 0.745122 | -0.03939 | 0.95036 | 0.95036 | 0.95036 | 0.95036 | 0.0 | 0.95036 | 0.54921 | 1.0 | 1.0 | 0.95036 | 1.67042 | | 11.01. | 0.1 | 1.806604 | 0.720061 | 0.679939 | -0.27042 | 0.71839 | 0.71839 | 0.71839 | 0.71839 | 0.0 | 0.71839 | 0.495781 | 0.1 | 1.0 | 0.71839 | 1.806604 | | 12.01. | 0.1 | 1.7156 | 1.088214 | 0.311786 | -0.406604 | 0.323424 | 0.323424 | 0.323424 | 0.323424 | 0.0 | 0.323424 | 0.476477 | 0.1 | 1.0 | 0.323424 | 1.7156 | | 13.01. | 0.1 | 1.579922 | 1.392176 | 0.007824 | -0.3156 | 0.03389 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.467837 | 0.1 | 1.1 | 0.2 | 1.579922 | | 14.01. | 0.1 | 1.488866 | 1.379922 | 0.020078 | -0.179922 | 0.100394 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.459197 | 0.1 | 1.2 | 0.2 | 1.488866 | | 15.01. | 0.1 | 1.525216 | 1.288866 | 0.111134 | -0.088866 | 0.264366 | 0.264366 | 0.264366 | 0.264366 | 0.0 | 0.264366 | 0.444996 | 0.1 | 1.3 | 0.264366 | 1.525216 | | 16.01. | 0.1 | 1.637612 | 1.260849 | 0.139151 | -0.125216 | 0.259326 | 0.259326 | 0.259326 | 0.259326 | 0.0 | 0.259326 | 0.43123 | 0.1 | 1.4 | 0.259326 | 1.637612 | | 17.01. | 0.1 | 1.74304 | 1.378286 | 0.021714 | -0.237612 | 0.072326 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.42259 | 0.1 | 1.5 | 0.2 | 1.74304 | | 18.01. | 0.1 | 1.824234 | 1.54304 | 0.0 | -0.34304 | 0.020494 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.41395 | 0.1 | 1.6 | 0.2 | 1.824234 | | 19.01. | 0.1 | 1.905933 | 1.624234 | 0.0 | -0.424234 | 0.009932 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.40531 | 0.1 | 1.7 | 0.2 | 1.905933 | | 20.01. | 0.1 | 2.0 | 1.705933 | 0.0 | -0.505933 | 0.004737 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.39667 | 0.1 | 1.8 | 0.2 | 2.0 |>>> restricttargetedrelease(True)Example 9
Another issue of the dam model relevant for the simulation of drought events to be discussed is the possible restriction of water release due to limited storage. To focus on this, we reset the parameter
NearDischargeMinimumThresholdto 0 m³/s and define smaller inflow values, which are constantly decreasing from 0.2 m³/s to 0.0 m³/s:>>> neardischargeminimumthreshold(0.0) >>> input_.sequences.sim.series = numpy.linspace(0.2, 0.0, 20)Now the storage content increases only until January, 5. Afterwards the dam begins to run dry. On January 11, the dam is actually empty. But there are some fluctuations of the water volume around 0 m³. The most severe deviation from the correct value of 0 m³ occurs on January 12, where the final storage volume is -666 m³:
Click here to see the graph>>> test("dam_v001_ex9") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 0.2 | 1.80075 | 1.9 | 0.0 | -0.5 | 0.005 | 0.005 | 0.005 | 0.00375 | 0.0 | 0.00375 | 0.016956 | 0.2 | 1.8 | 0.00375 | 1.80075 | | 02.01. | 0.189474 | 1.703953 | 1.797 | 0.0 | -0.40075 | 0.012265 | 0.012265 | 0.012265 | 0.012265 | 0.0 | 0.012265 | 0.032267 | 0.189474 | 1.7 | 0.012265 | 1.703953 | | 03.01. | 0.178947 | 1.611799 | 1.691688 | 0.0 | -0.303953 | 0.028841 | 0.028841 | 0.028841 | 0.028841 | 0.0 | 0.028841 | 0.045236 | 0.178947 | 1.6 | 0.028841 | 1.611799 | | 04.01. | 0.168421 | 1.528085 | 1.582958 | 0.0 | -0.211799 | 0.062468 | 0.062468 | 0.062468 | 0.062468 | 0.0 | 0.062468 | 0.05439 | 0.168421 | 1.5 | 0.062468 | 1.528085 | | 05.01. | 0.157895 | 1.458423 | 1.465616 | 0.0 | -0.128085 | 0.117784 | 0.117784 | 0.117784 | 0.117784 | 0.0 | 0.117784 | 0.057856 | 0.157895 | 1.4 | 0.117784 | 1.458423 | | 06.01. | 0.147368 | 1.417501 | 1.340639 | 0.059361 | -0.058423 | 0.243813 | 0.243813 | 0.243813 | 0.243813 | 0.0 | 0.243813 | 0.049523 | 0.147368 | 1.3 | 0.243813 | 1.417501 | | 07.01. | 0.136842 | 1.430358 | 1.173688 | 0.226312 | -0.017501 | 0.456251 | 0.456251 | 0.456251 | 0.456251 | 0.0 | 0.456251 | 0.021926 | 0.136842 | 1.2 | 0.456251 | 1.430358 | | 08.01. | 0.126316 | 1.443995 | 0.974107 | 0.425893 | -0.030358 | 0.641243 | 0.641243 | 0.641243 | 0.382861 | 0.0 | 0.382861 | -0.000239 | 0.126316 | 1.1 | 0.382861 | 1.443995 | | 09.01. | 0.115789 | 1.337495 | 1.061134 | 0.338866 | -0.043995 | 0.539003 | 0.539003 | 0.539003 | 0.11547 | 0.0 | 0.11547 | -0.000212 | 0.115789 | 1.0 | 0.11547 | 1.337495 | | 10.01. | 0.105263 | 1.228344 | 1.222025 | 0.177975 | 0.062505 | 0.497868 | 0.497868 | 0.497868 | 0.108362 | 0.0 | 0.108362 | -0.00048 | 0.105263 | 1.0 | 0.108362 | 1.228344 | | 11.01. | 0.094737 | 1.134148 | 1.119981 | 0.280019 | 0.171656 | 0.694448 | 0.694448 | 0.694448 | 0.089381 | 0.0 | 0.089381 | -0.000017 | 0.094737 | 1.0 | 0.089381 | 1.134148 | | 12.01. | 0.084211 | 1.098152 | 1.044768 | 0.355232 | 0.265852 | 0.815265 | 0.815265 | 0.815265 | 0.091721 | 0.0 | 0.091721 | -0.000666 | 0.084211 | 1.0 | 0.091721 | 1.098152 | | 13.01. | 0.073684 | 1.18792 | 1.006431 | 0.393569 | 0.301848 | 0.864198 | 0.864198 | 0.864198 | 0.067904 | 0.0 | 0.067904 | -0.000166 | 0.073684 | 1.1 | 0.067904 | 1.18792 | | 14.01. | 0.063158 | 1.277116 | 1.120015 | 0.279985 | 0.21208 | 0.717657 | 0.717657 | 0.717657 | 0.067501 | 0.0 | 0.067501 | -0.000542 | 0.063158 | 1.2 | 0.067501 | 1.277116 | | 15.01. | 0.052632 | 1.365852 | 1.209616 | 0.190384 | 0.122884 | 0.568242 | 0.568242 | 0.568242 | 0.046544 | 0.0 | 0.046544 | -0.000016 | 0.052632 | 1.3 | 0.046544 | 1.365852 | | 16.01. | 0.042105 | 1.455275 | 1.319309 | 0.080691 | 0.034148 | 0.369601 | 0.369601 | 0.369601 | 0.048083 | 0.0 | 0.048083 | -0.000532 | 0.042105 | 1.4 | 0.048083 | 1.455275 | | 17.01. | 0.031579 | 1.54538 | 1.407192 | 0.0 | -0.055275 | 0.187833 | 0.187833 | 0.187833 | 0.027168 | 0.0 | 0.027168 | -0.000151 | 0.031579 | 1.5 | 0.027168 | 1.54538 | | 18.01. | 0.021053 | 1.634293 | 1.518212 | 0.0 | -0.14538 | 0.104078 | 0.104078 | 0.104078 | 0.021731 | 0.0 | 0.021731 | -0.00021 | 0.021053 | 1.6 | 0.021731 | 1.634293 | | 19.01. | 0.010526 | 1.724252 | 1.612561 | 0.0 | -0.234293 | 0.052016 | 0.052016 | 0.052016 | 0.013004 | 0.0 | 0.013004 | -0.000424 | 0.010526 | 1.7 | 0.013004 | 1.724252 | | 20.01. | 0.0 | 1.814438 | 1.711248 | 0.0 | -0.324252 | 0.02417 | 0.02417 | 0.012085 | 0.0 | 0.0 | 0.0 | -0.000424 | 0.0 | 1.8 | 0.0 | 1.814438 |This behaviour of the dam model is due to method
Calc_ActualRelease_V1being involved in the set of differential equation that are solved approximately by a numerical integration algorithm. Theoretically, we could decrease the local truncation error to decrease this problem significantly. But this could result in quite huge computation times, as the underlying numerical algorithm is not really able to handle the discontinuous relationship between release and volume aroundNearDischargeMinimumThreshold.Example 10
One solution would be to define another version of the dam model and simply implement an alternative balance equation for the calculation of the actual release (not done yet, but seems to be worth the effort). When using the version of the dam model discussed here, it is instead advised to smooth this problematic discontinuity by increasing the value of parameter
NearDischargeMinimumTolerance(which could not be implemented properly if methodCalc_ActualRelease_V1would apply a simple balance equation):>>> waterlevelminimumtolerance(0.01)If one wants to avoid not only the fluctuation but also the negative values of the water volume, one should also sligthly increase the original threshold value, e.g.:
>>> waterlevelminimumthreshold(0.005)Now water storage is decaying smoothly. The lowest storage content of 541 m³ occurs on January 14. After that date, the dam is refilled to a certain degree. This is due the decreasing remote demand. Note that negative storage values are circumvented in this example, but this would have not been the case if the low flow period were prolonged:
Click here to see the graph>>> test("dam_v001_ex10") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 0.2 | 1.800256 | 1.9 | 0.0 | -0.5 | 0.005 | 0.005 | 0.005 | 0.001282 | 0.0 | 0.001282 | 0.017169 | 0.2 | 1.8 | 0.001282 | 1.800256 | | 02.01. | 0.189474 | 1.702037 | 1.798975 | 0.0 | -0.400256 | 0.01232 | 0.01232 | 0.01232 | 0.007624 | 0.0 | 0.007624 | 0.032881 | 0.189474 | 1.7 | 0.007624 | 1.702037 | | 03.01. | 0.178947 | 1.608618 | 1.694414 | 0.0 | -0.302037 | 0.029323 | 0.029323 | 0.029323 | 0.025921 | 0.0 | 0.025921 | 0.046103 | 0.178947 | 1.6 | 0.025921 | 1.608618 | | 04.01. | 0.168421 | 1.525188 | 1.582697 | 0.0 | -0.208618 | 0.064084 | 0.064084 | 0.064084 | 0.062022 | 0.0 | 0.062022 | 0.055296 | 0.168421 | 1.5 | 0.062022 | 1.525188 | | 05.01. | 0.157895 | 1.457043 | 1.463166 | 0.0 | -0.125188 | 0.120198 | 0.120198 | 0.120198 | 0.118479 | 0.0 | 0.118479 | 0.058701 | 0.157895 | 1.4 | 0.118479 | 1.457043 | | 06.01. | 0.147368 | 1.417039 | 1.338564 | 0.061436 | -0.057043 | 0.247367 | 0.247367 | 0.247367 | 0.242243 | 0.0 | 0.242243 | 0.050504 | 0.147368 | 1.3 | 0.242243 | 1.417039 | | 07.01. | 0.136842 | 1.418109 | 1.174796 | 0.225204 | -0.017039 | 0.45567 | 0.45567 | 0.45567 | 0.397328 | 0.0 | 0.397328 | 0.027998 | 0.136842 | 1.2 | 0.397328 | 1.418109 | | 08.01. | 0.126316 | 1.401604 | 1.020781 | 0.379219 | -0.018109 | 0.608464 | 0.608464 | 0.608464 | 0.290761 | 0.0 | 0.290761 | 0.01379 | 0.126316 | 1.1 | 0.290761 | 1.401604 | | 09.01. | 0.115789 | 1.290584 | 1.110843 | 0.289157 | -0.001604 | 0.537314 | 0.537314 | 0.537314 | 0.154283 | 0.0 | 0.154283 | 0.010464 | 0.115789 | 1.0 | 0.154283 | 1.290584 | | 10.01. | 0.105263 | 1.216378 | 1.136301 | 0.263699 | 0.109416 | 0.629775 | 0.629775 | 0.629775 | 0.138519 | 0.0 | 0.138519 | 0.007591 | 0.105263 | 1.0 | 0.138519 | 1.216378 | | 11.01. | 0.094737 | 1.15601 | 1.077859 | 0.322141 | 0.183622 | 0.744091 | 0.744091 | 0.744091 | 0.126207 | 0.0 | 0.126207 | 0.004871 | 0.094737 | 1.0 | 0.126207 | 1.15601 | | 12.01. | 0.084211 | 1.129412 | 1.029803 | 0.370197 | 0.24399 | 0.82219 | 0.82219 | 0.82219 | 0.109723 | 0.0 | 0.109723 | 0.002667 | 0.084211 | 1.0 | 0.109723 | 1.129412 | | 13.01. | 0.073684 | 1.214132 | 1.019689 | 0.380311 | 0.270588 | 0.841916 | 0.841916 | 0.841916 | 0.092645 | 0.0 | 0.092645 | 0.001029 | 0.073684 | 1.1 | 0.092645 | 1.214132 | | 14.01. | 0.063158 | 1.296357 | 1.121487 | 0.278513 | 0.185868 | 0.701812 | 0.701812 | 0.701812 | 0.068806 | 0.0 | 0.068806 | 0.000541 | 0.063158 | 1.2 | 0.068806 | 1.296357 | | 15.01. | 0.052632 | 1.376644 | 1.227551 | 0.172449 | 0.103643 | 0.533258 | 0.533258 | 0.533258 | 0.051779 | 0.0 | 0.051779 | 0.000615 | 0.052632 | 1.3 | 0.051779 | 1.376644 | | 16.01. | 0.042105 | 1.457718 | 1.324865 | 0.075135 | 0.023356 | 0.351863 | 0.351863 | 0.351863 | 0.035499 | 0.0 | 0.035499 | 0.001185 | 0.042105 | 1.4 | 0.035499 | 1.457718 | | 17.01. | 0.031579 | 1.540662 | 1.422218 | 0.0 | -0.057718 | 0.185207 | 0.185207 | 0.185207 | 0.02024 | 0.0 | 0.02024 | 0.002165 | 0.031579 | 1.5 | 0.02024 | 1.540662 | | 18.01. | 0.021053 | 1.626481 | 1.520422 | 0.0 | -0.140662 | 0.107697 | 0.107697 | 0.107697 | 0.012785 | 0.0 | 0.012785 | 0.002879 | 0.021053 | 1.6 | 0.012785 | 1.626481 | | 19.01. | 0.010526 | 1.71612 | 1.613695 | 0.0 | -0.226481 | 0.055458 | 0.055458 | 0.055458 | 0.006918 | 0.0 | 0.006918 | 0.003191 | 0.010526 | 1.7 | 0.006918 | 1.71612 | | 20.01. | 0.0 | 1.808953 | 1.709201 | 0.0 | -0.31612 | 0.025948 | 0.025948 | 0.012974 | 0.001631 | 0.0 | 0.001631 | 0.00305 | 0.0 | 1.8 | 0.001631 | 1.808953 |So the fluctuation seems to be gone, but there is still some inaccuracy in the results. Note that the last outflow value is smaller than the local truncation error. However, due to the smoothing of the discontinuous relationship it would now be possible to define a lower local truncation error without to increase computation times too much.
Example 11
The last “drought parameter” we did no not vary so far is
NmbLogEntries. In the examples above, this parameter was always set to 1, meaning that each estimate of the natural discharge of the subcatchment was based only on the latest observation. Using only the latest observation offers the advantage of quick adjustments of the control of the dam. But there is a risk of the estimates being too uncertain and of a bad timing of water releases during periods of fast fluctations.Let us define a series of extreme fluctuations by repeating the the natural discharge values of 1.5 m³/s and 0.5 m³/s ten times:
>>> natural.sequences.sim.series = 10*[1.5, 0.5]Also increase the inflow to 1 m³/s again, to assure that the dam is actually able to release as much water as has been estimated to be required:
>>> input_.sequences.sim.series = 1.0Furthermore, assume that there is no relevant routing time between the outlet of the dam and the cross section downstream:
>>> stream1.model.parameters.control.responses(((), (1.0,))) >>> stream1.model.parameters.update()The example is a little artificial, but reveals a general problem that might occur in different forms. Due to the time delay of the information flow from the cross section to the dam, much water is wasted to increase the peak flows, but the violations of the low flow threshold remain almost unchanged:
Click here to see the graph>>> test("dam_v001_ex11") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.502727 | 1.9 | 0.0 | -0.5 | 0.005 | 0.005 | 0.005 | 0.002727 | 0.0 | 0.002727 | 0.086164 | 1.0 | 1.5 | 0.002727 | 1.502727 | | 02.01. | 1.0 | 0.640003 | 1.5 | 0.0 | -0.102727 | 0.140038 | 0.140038 | 0.140038 | 0.140003 | 0.0 | 0.140003 | 0.160468 | 1.0 | 0.5 | 0.140003 | 0.640003 | | 03.01. | 1.0 | 2.899534 | 0.5 | 0.9 | 0.759997 | 1.399537 | 1.399537 | 1.399537 | 1.399534 | 0.0 | 1.399534 | 0.125948 | 1.0 | 1.5 | 1.399534 | 2.899534 | | 04.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499534 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.212348 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 05.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.177799 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 06.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.264199 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 07.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.22965 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 08.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.31605 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 09.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.281501 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 10.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.367901 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 11.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.333352 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 12.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.419752 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 13.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.385203 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 14.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.471603 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 15.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.437054 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 16.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.523454 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 17.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.488905 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 18.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.575305 | 1.0 | 0.5 | 0.000001 | 0.500001 | | 19.01. | 1.0 | 2.899872 | 0.5 | 0.9 | 0.899999 | 1.399872 | 1.399872 | 1.399872 | 1.399872 | 0.0 | 1.399872 | 0.540756 | 1.0 | 1.5 | 1.399872 | 2.899872 | | 20.01. | 1.0 | 0.500001 | 1.5 | 0.0 | -1.499872 | 0.000001 | 0.000001 | 0.000001 | 0.000001 | 0.0 | 0.000001 | 0.627156 | 1.0 | 0.5 | 0.000001 | 0.500001 |Example 12
It seems advisable to increase the number of observations taken into account to estimate the natural discharge at the cross section. For this purpose, the value of parameter
NmbLogEntriesis set to two days:>>> nmblogentries(2)Now the water release is relatively constant. This does not completely solve the problems of wasting water during peak flows and the repeated violation the low flow threshold, but reduces them significantly:
Click here to see the graph>>> test("dam_v001_ex12") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 1.0 | 1.502727 | 1.9 | 0.0 | -0.5 | 0.005 | 0.005 | 0.005 | 0.002727 | 0.0 | 0.002727 | 0.086164 | 1.0 | 1.5 | 0.002727 | 1.502727 | | 02.01. | 1.0 | 0.529487 | 1.7 | 0.0 | -0.301364 | 0.029495 | 0.029495 | 0.029495 | 0.029487 | 0.0 | 0.029487 | 0.170017 | 1.0 | 0.5 | 0.029487 | 0.529487 | | 03.01. | 1.0 | 2.385738 | 1.0 | 0.4 | 0.383893 | 0.885738 | 0.885738 | 0.885738 | 0.885738 | 0.0 | 0.885738 | 0.179889 | 1.0 | 1.5 | 0.885738 | 2.385738 | | 04.01. | 1.0 | 1.08532 | 1.0 | 0.4 | -0.057613 | 0.58532 | 0.58532 | 0.58532 | 0.58532 | 0.0 | 0.58532 | 0.215717 | 1.0 | 0.5 | 0.58532 | 1.08532 | | 05.01. | 1.0 | 1.921895 | 1.0 | 0.4 | -0.335529 | 0.421895 | 0.421895 | 0.421895 | 0.421895 | 0.0 | 0.421895 | 0.265666 | 1.0 | 1.5 | 0.421895 | 1.921895 | | 06.01. | 1.0 | 1.039224 | 1.0 | 0.4 | -0.103607 | 0.539224 | 0.539224 | 0.539224 | 0.539224 | 0.0 | 0.539224 | 0.305477 | 1.0 | 0.5 | 0.539224 | 1.039224 | | 07.01. | 1.0 | 2.061463 | 1.0 | 0.4 | -0.080559 | 0.561463 | 0.561463 | 0.561463 | 0.561463 | 0.0 | 0.561463 | 0.343366 | 1.0 | 1.5 | 0.561463 | 2.061463 | | 08.01. | 1.0 | 1.000369 | 1.0 | 0.4 | -0.150343 | 0.500369 | 0.500369 | 0.500369 | 0.500369 | 0.0 | 0.500369 | 0.386534 | 1.0 | 0.5 | 0.500369 | 1.000369 | | 09.01. | 1.0 | 2.015458 | 1.0 | 0.4 | -0.130916 | 0.515458 | 0.515458 | 0.515458 | 0.515458 | 0.0 | 0.515458 | 0.428399 | 1.0 | 1.5 | 0.515458 | 2.015458 | | 10.01. | 1.0 | 1.035283 | 1.0 | 0.4 | -0.107913 | 0.535283 | 0.535283 | 0.535283 | 0.535283 | 0.0 | 0.535283 | 0.46855 | 1.0 | 0.5 | 0.535283 | 1.035283 | | 11.01. | 1.0 | 2.020045 | 1.0 | 0.4 | -0.125371 | 0.520045 | 0.520045 | 0.520045 | 0.520045 | 0.0 | 0.520045 | 0.510018 | 1.0 | 1.5 | 0.520045 | 2.020045 | | 12.01. | 1.0 | 1.018133 | 1.0 | 0.4 | -0.127664 | 0.518133 | 0.518133 | 0.518133 | 0.518133 | 0.0 | 0.518133 | 0.551652 | 1.0 | 0.5 | 0.518133 | 1.018133 | | 13.01. | 1.0 | 2.02539 | 1.0 | 0.4 | -0.119089 | 0.52539 | 0.52539 | 0.52539 | 0.52539 | 0.0 | 0.52539 | 0.592658 | 1.0 | 1.5 | 0.52539 | 2.02539 | | 14.01. | 1.0 | 1.023097 | 1.0 | 0.4 | -0.121761 | 0.523097 | 0.523097 | 0.523097 | 0.523097 | 0.0 | 0.523097 | 0.633863 | 1.0 | 0.5 | 0.523097 | 1.023097 | | 15.01. | 1.0 | 2.020992 | 1.0 | 0.4 | -0.124244 | 0.520992 | 0.520992 | 0.520992 | 0.520992 | 0.0 | 0.520992 | 0.675249 | 1.0 | 1.5 | 0.520992 | 2.020992 | | 16.01. | 1.0 | 1.022855 | 1.0 | 0.4 | -0.122045 | 0.522855 | 0.522855 | 0.522855 | 0.522855 | 0.0 | 0.522855 | 0.716474 | 1.0 | 0.5 | 0.522855 | 1.022855 | | 17.01. | 1.0 | 2.022958 | 1.0 | 0.4 | -0.121924 | 0.522958 | 0.522958 | 0.522958 | 0.522958 | 0.0 | 0.522958 | 0.75769 | 1.0 | 1.5 | 0.522958 | 2.022958 | | 18.01. | 1.0 | 1.022123 | 1.0 | 0.4 | -0.122907 | 0.522123 | 0.522123 | 0.522123 | 0.522123 | 0.0 | 0.522123 | 0.798979 | 1.0 | 0.5 | 0.522123 | 1.022123 | | 19.01. | 1.0 | 2.022434 | 1.0 | 0.4 | -0.12254 | 0.522434 | 0.522434 | 0.522434 | 0.522434 | 0.0 | 0.522434 | 0.840241 | 1.0 | 1.5 | 0.522434 | 2.022434 | | 20.01. | 1.0 | 1.022657 | 1.0 | 0.4 | -0.122278 | 0.522657 | 0.522657 | 0.522657 | 0.522657 | 0.0 | 0.522657 | 0.881483 | 1.0 | 0.5 | 0.522657 | 1.022657 |Such negative effects due to information delay cannot be circumvented easily, unless one would solve the differential equations of all models involved simultaneously. However, at least for drougth events (with much slower dynamics than flood events) these delays should normally be not overly important.
Example 13
This and the following examples are supposed to demonstrate that the flood retention methods are implemented properly. Hence, all parameters related to low water calculations are set in a deactivating manner:
>>> nmblogentries(1) >>> remotedischargeminimum(0.0) >>> remotedischargesafety(0.0) >>> neardischargeminimumthreshold(0.0) >>> neardischargeminimumtolerance(0.0) >>> waterlevelminimumthreshold(0.0) >>> waterlevelminimumtolerance(0.0)To be able to compare the following numerical results of HydPy-Dam with an analytical solution, we define a linear storage retetenion process. The relationship between water level and volume has already been defined to be linear and we do the same for the relationship between flood discharge and water level:
>>> waterlevel2flooddischarge(ann( ... weights_input=1.0, weights_output=2.5, ... intercepts_hidden=0.0, intercepts_output=0.0, ... activation=0)) >>> waterlevel2flooddischarge.plot(0.0, 25.0) >>> save_autofig("dam_v001_waterlevel2flooddischarge_2.png")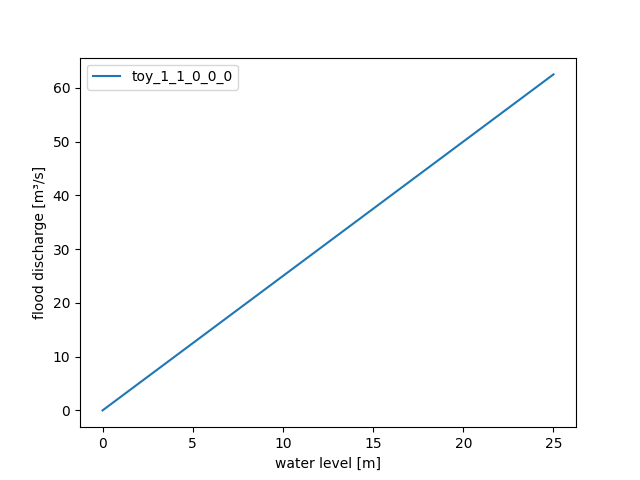
Hence, for the given simulation step size, the linear storage coefficient is approximately 0.054 per day.
Now a flood event needs to be defined:
>>> input_.sequences.sim.series = [ 0., 1., 5., 9., 8., 5., 3., 2., 1., 0., ... 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]For the sake of simplicity, a constant discharge of 1 m³/s of the subcatchment is assumed:
>>> test.inits.loggedtotalremotedischarge = 1.0 >>> natural.sequences.sim.series = 1.0At first, a low numerical accuracy of 0.01 m³/s is defined, which should be sufficient for most flood simulations for large dams:
>>> solver.abserrormax(1e-2)When simulating flood events, numerical stability and accuracy and their relation to computation time should be examined more closely. We use the number of function calls of the set of differential equations as an indicator for computation time, and set the corresponding counter to zero:
>>> model.numvars.nmb_calls = 0You can plot this table to see that the dam actually responds (approximately) like a linear storage:
Click here to see the graph>>> test("dam_v001_ex13") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | | 02.01. | 1.0 | 1.026514 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.026514 | 0.026514 | 0.084109 | 1.0 | 1.0 | 0.026514 | 1.026514 | | 03.01. | 5.0 | 1.183744 | 1.0 | 0.0 | -1.026514 | 0.0 | 0.0 | 0.0 | 0.0 | 0.183744 | 0.183744 | 0.500234 | 5.0 | 1.0 | 0.183744 | 1.183744 | | 04.01. | 9.0 | 1.542983 | 1.0 | 0.0 | -1.183744 | 0.0 | 0.0 | 0.0 | 0.0 | 0.542983 | 0.542983 | 1.23092 | 9.0 | 1.0 | 0.542983 | 1.542983 | | 05.01. | 8.0 | 1.961039 | 1.0 | 0.0 | -1.542983 | 0.0 | 0.0 | 0.0 | 0.0 | 0.961039 | 0.961039 | 1.839086 | 8.0 | 1.0 | 0.961039 | 1.961039 | | 06.01. | 5.0 | 2.251523 | 1.0 | 0.0 | -1.961039 | 0.0 | 0.0 | 0.0 | 0.0 | 1.251523 | 1.251523 | 2.162955 | 5.0 | 1.0 | 1.251523 | 2.251523 | | 07.01. | 3.0 | 2.395546 | 1.0 | 0.0 | -2.251523 | 0.0 | 0.0 | 0.0 | 0.0 | 1.395546 | 1.395546 | 2.301579 | 3.0 | 1.0 | 1.395546 | 2.395546 | | 08.01. | 2.0 | 2.453375 | 1.0 | 0.0 | -2.395546 | 0.0 | 0.0 | 0.0 | 0.0 | 1.453375 | 1.453375 | 2.348808 | 2.0 | 1.0 | 1.453375 | 2.453375 | | 09.01. | 1.0 | 2.455596 | 1.0 | 0.0 | -2.453375 | 0.0 | 0.0 | 0.0 | 0.0 | 1.455596 | 1.455596 | 2.309444 | 1.0 | 1.0 | 1.455596 | 2.455596 | | 10.01. | 0.0 | 2.405132 | 1.0 | 0.0 | -2.455596 | 0.0 | 0.0 | 0.0 | 0.0 | 1.405132 | 1.405132 | 2.188041 | 0.0 | 1.0 | 1.405132 | 2.405132 | | 11.01. | 0.0 | 2.331267 | 1.0 | 0.0 | -2.405132 | 0.0 | 0.0 | 0.0 | 0.0 | 1.331267 | 1.331267 | 2.073019 | 0.0 | 1.0 | 1.331267 | 2.331267 | | 12.01. | 0.0 | 2.261285 | 1.0 | 0.0 | -2.331267 | 0.0 | 0.0 | 0.0 | 0.0 | 1.261285 | 1.261285 | 1.964044 | 0.0 | 1.0 | 1.261285 | 2.261285 | | 13.01. | 0.0 | 2.194981 | 1.0 | 0.0 | -2.261285 | 0.0 | 0.0 | 0.0 | 0.0 | 1.194981 | 1.194981 | 1.860798 | 0.0 | 1.0 | 1.194981 | 2.194981 | | 14.01. | 0.0 | 2.132163 | 1.0 | 0.0 | -2.194981 | 0.0 | 0.0 | 0.0 | 0.0 | 1.132163 | 1.132163 | 1.762979 | 0.0 | 1.0 | 1.132163 | 2.132163 | | 15.01. | 0.0 | 2.072647 | 1.0 | 0.0 | -2.132163 | 0.0 | 0.0 | 0.0 | 0.0 | 1.072647 | 1.072647 | 1.670302 | 0.0 | 1.0 | 1.072647 | 2.072647 | | 16.01. | 0.0 | 2.01626 | 1.0 | 0.0 | -2.072647 | 0.0 | 0.0 | 0.0 | 0.0 | 1.01626 | 1.01626 | 1.582498 | 0.0 | 1.0 | 1.01626 | 2.01626 | | 17.01. | 0.0 | 1.962837 | 1.0 | 0.0 | -2.01626 | 0.0 | 0.0 | 0.0 | 0.0 | 0.962837 | 0.962837 | 1.499308 | 0.0 | 1.0 | 0.962837 | 1.962837 | | 18.01. | 0.0 | 1.912222 | 1.0 | 0.0 | -1.962837 | 0.0 | 0.0 | 0.0 | 0.0 | 0.912222 | 0.912222 | 1.420492 | 0.0 | 1.0 | 0.912222 | 1.912222 | | 19.01. | 0.0 | 1.864268 | 1.0 | 0.0 | -1.912222 | 0.0 | 0.0 | 0.0 | 0.0 | 0.864268 | 0.864268 | 1.34582 | 0.0 | 1.0 | 0.864268 | 1.864268 | | 20.01. | 0.0 | 1.818835 | 1.0 | 0.0 | -1.864268 | 0.0 | 0.0 | 0.0 | 0.0 | 0.818835 | 0.818835 | 1.275072 | 0.0 | 1.0 | 0.818835 | 1.818835 |For a more precise evaluation, you can compare the outflow of the dam with the following results of the linear storage cascade with only one storage:
>>> from hydpy.auxs.iuhtools import LinearStorageCascade >>> lsc = LinearStorageCascade(n=1, k=1.0/0.054) >>> round_(numpy.convolve(lsc.ma.coefs, input_.sequences.sim.series)[:20]) 0.0, 0.02652, 0.183776, 0.543037, 0.961081, 1.251541, 1.395548, 1.453371, 1.455585, 1.405116, 1.331252, 1.261271, 1.194968, 1.132151, 1.072636, 1.01625, 0.962828, 0.912214, 0.864261, 0.818829The largest difference occurs on January, 1. But this difference of 0.000054 m³/s is way below the required accuracy of 0.01 m³/s. There is no guarantee that the actual numerical error will always fall below the defined tolerance value. However, if everything works well, we should at least expect so for the individual simulation time step, as the actual error should be better as the error estimate by one order. On the other hand, the accumulation of errors of individual simulation time steps is not controlled and might sometimes result in an violation of the defined tolerance value.
To achieve the results discussed above, about 4 calls of the methods of the dam model were required:
>>> model.numvars.nmb_calls 78 >>> model.numvars.nmb_calls = 0Example 14
If we set the tolerance value to 1e-6 m³/s, the printed table shows (six decimal places) no deviation from the analytical solution of the linear storage:
Click here to see the graph>>> solver.abserrormax(1e-6) >>> test("dam_v001_ex14") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | | 02.01. | 1.0 | 1.02652 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.02652 | 0.02652 | 0.084109 | 1.0 | 1.0 | 0.02652 | 1.02652 | | 03.01. | 5.0 | 1.183776 | 1.0 | 0.0 | -1.02652 | 0.0 | 0.0 | 0.0 | 0.0 | 0.183776 | 0.183776 | 0.50023 | 5.0 | 1.0 | 0.183776 | 1.183776 | | 04.01. | 9.0 | 1.543037 | 1.0 | 0.0 | -1.183776 | 0.0 | 0.0 | 0.0 | 0.0 | 0.543037 | 0.543037 | 1.230912 | 9.0 | 1.0 | 0.543037 | 1.543037 | | 05.01. | 8.0 | 1.961081 | 1.0 | 0.0 | -1.543037 | 0.0 | 0.0 | 0.0 | 0.0 | 0.961081 | 0.961081 | 1.839075 | 8.0 | 1.0 | 0.961081 | 1.961081 | | 06.01. | 5.0 | 2.251541 | 1.0 | 0.0 | -1.961081 | 0.0 | 0.0 | 0.0 | 0.0 | 1.251541 | 1.251541 | 2.162941 | 5.0 | 1.0 | 1.251541 | 2.251541 | | 07.01. | 3.0 | 2.395548 | 1.0 | 0.0 | -2.251541 | 0.0 | 0.0 | 0.0 | 0.0 | 1.395548 | 1.395548 | 2.301566 | 3.0 | 1.0 | 1.395548 | 2.395548 | | 08.01. | 2.0 | 2.453371 | 1.0 | 0.0 | -2.395548 | 0.0 | 0.0 | 0.0 | 0.0 | 1.453371 | 1.453371 | 2.348795 | 2.0 | 1.0 | 1.453371 | 2.453371 | | 09.01. | 1.0 | 2.455585 | 1.0 | 0.0 | -2.453371 | 0.0 | 0.0 | 0.0 | 0.0 | 1.455585 | 1.455585 | 2.309432 | 1.0 | 1.0 | 1.455585 | 2.455585 | | 10.01. | 0.0 | 2.405116 | 1.0 | 0.0 | -2.455585 | 0.0 | 0.0 | 0.0 | 0.0 | 1.405116 | 1.405116 | 2.18803 | 0.0 | 1.0 | 1.405116 | 2.405116 | | 11.01. | 0.0 | 2.331252 | 1.0 | 0.0 | -2.405116 | 0.0 | 0.0 | 0.0 | 0.0 | 1.331252 | 1.331252 | 2.07301 | 0.0 | 1.0 | 1.331252 | 2.331252 | | 12.01. | 0.0 | 2.261271 | 1.0 | 0.0 | -2.331252 | 0.0 | 0.0 | 0.0 | 0.0 | 1.261271 | 1.261271 | 1.964036 | 0.0 | 1.0 | 1.261271 | 2.261271 | | 13.01. | 0.0 | 2.194968 | 1.0 | 0.0 | -2.261271 | 0.0 | 0.0 | 0.0 | 0.0 | 1.194968 | 1.194968 | 1.860791 | 0.0 | 1.0 | 1.194968 | 2.194968 | | 14.01. | 0.0 | 2.132151 | 1.0 | 0.0 | -2.194968 | 0.0 | 0.0 | 0.0 | 0.0 | 1.132151 | 1.132151 | 1.762973 | 0.0 | 1.0 | 1.132151 | 2.132151 | | 15.01. | 0.0 | 2.072636 | 1.0 | 0.0 | -2.132151 | 0.0 | 0.0 | 0.0 | 0.0 | 1.072636 | 1.072636 | 1.670297 | 0.0 | 1.0 | 1.072636 | 2.072636 | | 16.01. | 0.0 | 2.01625 | 1.0 | 0.0 | -2.072636 | 0.0 | 0.0 | 0.0 | 0.0 | 1.01625 | 1.01625 | 1.582493 | 0.0 | 1.0 | 1.01625 | 2.01625 | | 17.01. | 0.0 | 1.962828 | 1.0 | 0.0 | -2.01625 | 0.0 | 0.0 | 0.0 | 0.0 | 0.962828 | 0.962828 | 1.499305 | 0.0 | 1.0 | 0.962828 | 1.962828 | | 18.01. | 0.0 | 1.912214 | 1.0 | 0.0 | -1.962828 | 0.0 | 0.0 | 0.0 | 0.0 | 0.912214 | 0.912214 | 1.42049 | 0.0 | 1.0 | 0.912214 | 1.912214 | | 19.01. | 0.0 | 1.864261 | 1.0 | 0.0 | -1.912214 | 0.0 | 0.0 | 0.0 | 0.0 | 0.864261 | 0.864261 | 1.345818 | 0.0 | 1.0 | 0.864261 | 1.864261 | | 20.01. | 0.0 | 1.818829 | 1.0 | 0.0 | -1.864261 | 0.0 | 0.0 | 0.0 | 0.0 | 0.818829 | 0.818829 | 1.275071 | 0.0 | 1.0 | 0.818829 | 1.818829 |However, this improvement in accuracy increases the computation time significantly. Now 10.5 calls were required on average:
>>> model.numvars.nmb_calls 211 >>> model.numvars.nmb_calls = 0Example 15
Now we reset the local error tolerance to the more realistic value. But we configure the
WaterLevel2FloodDischargeparameter in a highly reactive manner:>>> solver.abserrormax(1e-2) >>> waterlevel2flooddischarge(ann( ... weights_input=1.0, weights_output=250.0, ... intercepts_hidden=0.0, intercepts_output=0.0, ... activation=0)) >>> waterlevel2flooddischarge.plot(0.0, 25.0) >>> save_autofig("dam_v001_waterlevel2flooddischarge_3.png")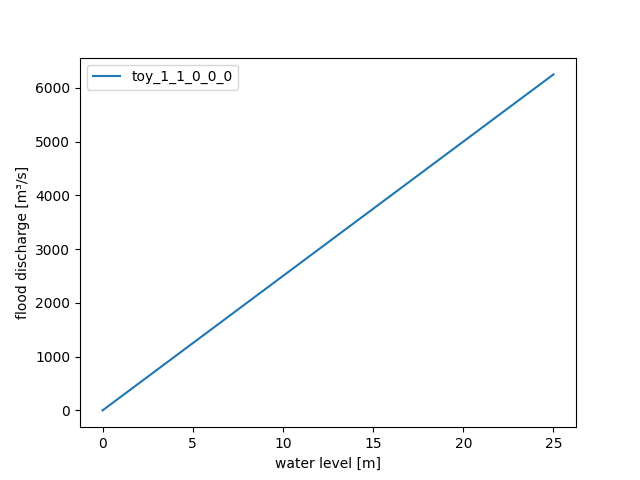
With this new parameterization of the dam model, the linear storage coefficient is approximately 5.4 per day. This is why the following test results show virtually no retention effects:
Click here to see the graph>>> test("dam_v001_ex15") | date | inflow | totalremotedischarge | naturalremotedischarge | remotedemand | remotefailure | requiredremoterelease | requiredrelease | targetedrelease | actualrelease | flooddischarge | outflow | watervolume | input_ | natural | output | remote | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | 01.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | | 02.01. | 1.0 | 1.818699 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.818699 | 0.818699 | 0.015664 | 1.0 | 1.0 | 0.818699 | 1.818699 | | 03.01. | 5.0 | 5.25814 | 1.0 | 0.0 | -1.818699 | 0.0 | 0.0 | 0.0 | 0.0 | 4.25814 | 4.25814 | 0.079761 | 5.0 | 1.0 | 4.25814 | 5.25814 | | 04.01. | 9.0 | 9.259255 | 1.0 | 0.0 | -5.25814 | 0.0 | 0.0 | 0.0 | 0.0 | 8.259255 | 8.259255 | 0.143761 | 9.0 | 1.0 | 8.259255 | 9.259255 | | 05.01. | 8.0 | 9.178598 | 1.0 | 0.0 | -9.259255 | 0.0 | 0.0 | 0.0 | 0.0 | 8.178598 | 8.178598 | 0.128331 | 8.0 | 1.0 | 8.178598 | 9.178598 | | 06.01. | 5.0 | 6.555424 | 1.0 | 0.0 | -9.178598 | 0.0 | 0.0 | 0.0 | 0.0 | 5.555424 | 5.555424 | 0.080342 | 5.0 | 1.0 | 5.555424 | 6.555424 | | 07.01. | 3.0 | 4.371696 | 1.0 | 0.0 | -6.555424 | 0.0 | 0.0 | 0.0 | 0.0 | 3.371696 | 3.371696 | 0.048227 | 3.0 | 1.0 | 3.371696 | 4.371696 | | 08.01. | 2.0 | 3.183878 | 1.0 | 0.0 | -4.371696 | 0.0 | 0.0 | 0.0 | 0.0 | 2.183878 | 2.183878 | 0.03234 | 2.0 | 1.0 | 2.183878 | 3.183878 | | 09.01. | 1.0 | 2.185158 | 1.0 | 0.0 | -3.183878 | 0.0 | 0.0 | 0.0 | 0.0 | 1.185158 | 1.185158 | 0.016343 | 1.0 | 1.0 | 1.185158 | 2.185158 | | 10.01. | 0.0 | 1.188656 | 1.0 | 0.0 | -2.185158 | 0.0 | 0.0 | 0.0 | 0.0 | 0.187346 | 0.188656 | 0.000043 | 0.0 | 1.0 | 0.188656 | 1.188656 | | 11.01. | 0.0 | 1.001338 | 1.0 | 0.0 | -1.188656 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.001338 | -0.000073 | 0.0 | 1.0 | 0.001338 | 1.001338 | | 12.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.001338 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 13.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 14.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 15.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 16.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 17.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 18.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 19.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 | | 20.01. | 0.0 | 1.0 | 1.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 0.0 | -0.00455 | 0.0 | -0.000073 | 0.0 | 1.0 | 0.0 | 1.0 |The following calculations show that the dam model reaches the required numerical for this extreme parameterizations:
>>> lsc.k = 1.0/5.4 >>> round_(numpy.convolve(lsc.ma.coefs, input_.sequences.sim.series)[:20]) 0.0, 0.815651, 4.261772, 8.259271, 8.181003, 5.553864, 3.371199, 2.186025, 1.185189, 0.185185, 0.000836, 0.000004, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0However, due to the potential stiffness of this parameterization, the division of the different simulation steps into some substeps were required. This increased the average required number of model methods calls to 19 per simulation step:
>>> model.numvars.nmb_calls 358 >>> model.numvars.nmb_calls = 0Also note that the final water volume is negative due the limited numerical accuracy of the results.
For common (realistic) simulations of dam retention processes, the stability issue disussed here should not be of big relevance. But one should keep it in mind when playing around with parameters e.g. during model calibration. Otherwise unexpectedly long simulation durations might occur.
-
class
hydpy.models.dam_v001.Model[source]¶ Bases:
hydpy.core.modeltools.ELSModelVersion 1 of HydPy-Dam.
- The following “receiver update methods” are called in the given sequence before performing a simulation step:
Pic_TotalRemoteDischarge_V1Update the receiver link sequence.Update_LoggedTotalRemoteDischarge_V1Log a new entry of discharge at a cross section far downstream.
- The following “inlet update methods” are called in the given sequence at the beginning of each simulation step:
Pic_Inflow_V1Update the inlet link sequence.Calc_NaturalRemoteDischarge_V1Try to estimate the natural discharge of a cross section far downstream based on the last few simulation steps.Calc_RemoteDemand_V1Estimate the discharge demand of a cross section far downstream.Calc_RemoteFailure_V1Estimate the shortfall of actual discharge under the required discharge of a cross section far downstream.Calc_RequiredRemoteRelease_V1Guess the required release necessary to not fall below the threshold value at a cross section far downstream with a certain level of certainty.Calc_RequiredRelease_V1Calculate the total water release (immediately and far downstream) required for reducing drought events.Calc_TargetedRelease_V1Calculate the targeted water release for reducing drought events, taking into account both the required water release and the actual inflow into the dam.
- The following methods define the relevant components of a system of ODE equations (e.g. direct runoff):
Pic_Inflow_V1Update the inlet link sequence.Calc_WaterLevel_V1Determine the water level based on an artificial neural network describing the relationship between water level and water stage.Calc_ActualRelease_V1Calculate the actual water release that can be supplied by the dam considering the targeted release and the given water level.Calc_FloodDischarge_V1Calculate the discharge during and after a flood event based on anSeasonalANNdescribing the relationship(s) between discharge and water stage.Calc_Outflow_V1Calculate the total outflow of the dam.
- The following methods define the complete equations of an ODE system (e.g. change in storage of fast water due to effective precipitation and direct runoff):
Update_WaterVolume_V1Update the actual water volume.
- The following “outlet update methods” are called in the given sequence at the end of each simulation step:
Pass_Outflow_V1Update the outlet link sequenceQ.Update_LoggedOutflow_V1Log a new entry of discharge at a cross section far downstream.
-
numconsts: hydpy.core.modeltools.NumConstsELS¶
-
numvars: hydpy.core.modeltools.NumVarsELS¶
-
class
hydpy.models.dam_v001.AideSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.ModelSequences[AideSequence,hydpy.core.variabletools.FastAccess]Aide sequences of model dam_v001.
- The following classes are selected:
WaterLevel()Water level [m].
-
class
hydpy.models.dam_v001.ControlParameters(master: hydpy.core.parametertools.Parameters, cls_fastaccess: Optional[Type[hydpy.core.parametertools.FastAccessParameter]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.variabletools.SubVariables[hydpy.core.parametertools.Parameters,Parameter,hydpy.core.parametertools.FastAccessParameter]Control parameters of model dam_v001.
- The following classes are selected:
CatchmentArea()Size of the catchment draining into the dam [km²].NmbLogEntries()Number of log entries for certain variables [-].RemoteDischargeMinimum()Discharge threshold of a cross section far downstream that should not be undercut by the actual discharge [m³/s].RemoteDischargeSafety()Safety factor to reduce the risk to release not enough water [m³/s].NearDischargeMinimumThreshold()Discharge threshold of a cross section in the near of the dam that not be undercut by the actual discharge [m³/s].NearDischargeMinimumTolerance()A tolerance value for the “near discharge minimum” [m³/s].RestrictTargetedRelease()A flag indicating whether low flow variability has to be preserved or not [-].WaterLevelMinimumThreshold()The minimum operating water level of the dam [m].WaterLevelMinimumTolerance()A tolarance value for the minimum operating water level [m].WaterVolume2WaterLevel()Artificial neural network describing the relationship between water level and water volume [-].WaterLevel2FloodDischarge()Artificial neural network describing the relationship between flood discharge and water volume [-].
-
class
hydpy.models.dam_v001.DerivedParameters(master: hydpy.core.parametertools.Parameters, cls_fastaccess: Optional[Type[hydpy.core.parametertools.FastAccessParameter]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.variabletools.SubVariables[hydpy.core.parametertools.Parameters,Parameter,hydpy.core.parametertools.FastAccessParameter]Derived parameters of model dam_v001.
- The following classes are selected:
TOY()References thetimeofyearindex array provided by the instance of classIndexeravailable in modulepub. [-].Seconds()Length of the actual simulation step size in seconds [s].RemoteDischargeSmoothPar()Smoothing parameter to be derived fromRemoteDischargeSafety[m³/s].NearDischargeMinimumSmoothPar1()Smoothing parameter to be derived fromNearDischargeMinimumThresholdfor smoothing kernelsmooth_logistic1()[m³/s].NearDischargeMinimumSmoothPar2()Smoothing parameter to be derived fromNearDischargeMinimumThresholdfor smoothing kernelsmooth_logistic2()[m³/s].WaterLevelMinimumSmoothPar()Smoothing parameter to be derived fromWaterLevelMinimumTolerancefor smoothing kernelsmooth_logistic1()[m].
-
class
hydpy.models.dam_v001.FluxSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.OutputSequences[FluxSequence]Flux sequences of model dam_v001.
- The following classes are selected:
Inflow()Total inflow [m³/s].TotalRemoteDischarge()Total discharge at a cross section far downstream [m³/s].NaturalRemoteDischarge()Natural discharge at a cross section far downstream [m³/s].RemoteDemand()Discharge demand at a cross section far downstream [m³/s].RemoteFailure()Difference between the the actual and the required discharge at a cross section far downstream [m³/s].RequiredRemoteRelease()Water release considered appropriate to reduce drought events at cross sections far downstream to the desired degree [m³/s].RequiredRelease()Required water release for reducing drought events downstream [m³/s].TargetedRelease()The targeted water release for reducing drought events downstream after taking both the required release and additional low flow regulations into account [m³/s].ActualRelease()Actual water release thought for reducing drought events downstream [m³/s].FloodDischarge()Water release associated with flood events [m³/s].Outflow()Total outflow [m³/s].
-
class
hydpy.models.dam_v001.InletSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.LinkSequences[InletSequence]Inlet sequences of model dam_v001.
- The following classes are selected:
Q()Discharge [m³/s].
-
class
hydpy.models.dam_v001.LogSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.ModelSequences[LogSequence,hydpy.core.variabletools.FastAccess]Log sequences of model dam_v001.
- The following classes are selected:
LoggedTotalRemoteDischarge()Logged discharge values from somewhere else [m3/s].LoggedOutflow()Logged discharge values from the dam itself [m3/s].
-
class
hydpy.models.dam_v001.OutletSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.LinkSequences[OutletSequence]Outlet sequences of model dam_v001.
- The following classes are selected:
Q()Discharge [m³/s].
-
class
hydpy.models.dam_v001.ReceiverSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.LinkSequences[ReceiverSequence]Receiver sequences of model dam_v001.
- The following classes are selected:
Q()Discharge [m³/s].
-
class
hydpy.models.dam_v001.SolverParameters(master: hydpy.core.parametertools.Parameters, cls_fastaccess: Optional[Type[hydpy.core.parametertools.FastAccessParameter]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.variabletools.SubVariables[hydpy.core.parametertools.Parameters,Parameter,hydpy.core.parametertools.FastAccessParameter]Solver parameters of model dam_v001.
- The following classes are selected:
AbsErrorMax()Absolute numerical error tolerance [m3/s].RelErrorMax()Relative numerical error tolerance [1/T].RelDTMin()Smallest relative integration time step size allowed [-].RelDTMax()Largest relative integration time step size allowed [-].
-
class
hydpy.models.dam_v001.StateSequences(master: hydpy.core.sequencetools.Sequences, cls_fastaccess: Optional[Type[FastAccessType]] = None, cymodel: Optional[hydpy.core.typingtools.CyModelProtocol] = None)¶ Bases:
hydpy.core.sequencetools.OutputSequences[StateSequence]State sequences of model dam_v001.
- The following classes are selected:
WaterVolume()Water volume [million m³].
