HydPy-Dam-V1 (dam model, version 1)

dam_v001 is supposed to represent a dam with an “active” low water control scheme and a “passive” high water control scheme.

During low flow conditions, dam_v001 tries to increase low runoff values immediately downstream the of dam and at a more remote location in the downstream river channel. The latter requires that dam_v001 receives information from downstream via a “receiver node”. To achieve reliable drought control, dam_v001 stores some low-flow related information for several simulation steps.

During high flow conditions, dam_v001 is controlled by two relationships: one between water volume and water level, and the other between discharge and water level. While the first one is stationary, the second one can vary seasonally. In both cases, one defines these relationships via interpolators. See the documentation on the classes PPoly and ANN, which explains how to configure stepwise linear, spline, or neural network-based interpolations.

dam_v001 solves its differential equation with an adaptive Runge-Kutta method that only works well on continuous equations. Hence, we defined most threshold-based low-flow equations in a “smoothable” manner. However, defining realistic and computationally efficient configurations of the related smoothing parameters requires some experience. Therefore, it seems advisable to investigate the functioning of each new model parameterisation on several synthetic or measured drought events.

The applied solver is an explicit Runge-Kutta method unsuitable for stiff initial value problems. Its adaptive order and stepsize control prevent inaccurate results caused by stability issues. But for very responsive dams, increased computation times are possible. We come back to this point at the end of this section.

By default, dam_v001 neither takes precipitation nor evaporation into account, but you can add submodels that comply with the PrecipModel_V2 or PETModel_V1 interface that supply this information.

Integration tests

Note

When new to HydPy, consider reading section Integration Tests first.

We perform all of the following examples over 20 days:

>>> from hydpy import pub
>>> pub.timegrids = "01.01.2000", "21.01.2000", "1d"

The first examples demonstrate how dam_v001 reduces drought events at a cross-section far downstream under different configurations. In real cases, this requires taking the travel time of the released water into account. Therefore, we will use the arma_rimorido application model to route the dam’s outflow to the cross-section under investigation. Furthermore, we add some “natural” discharge to the cross-section, reflecting the influence of the subcatchment between the dam and the cross-section.

We define four Node objects:

  • Node ‘inflow’ passes the inflow into the dam.

  • Node ‘natural’ handles the subcatchment’s additional discharge.

  • Node ‘outflow’ receives the dam’s (unmodified) outflow.

  • Node ‘remote’ receives the dam’s routed outflow and the subcatchment’s additional discharge.

>>> from hydpy import Node
>>> inflow = Node("inflow")
>>> outflow = Node("outflow")
>>> natural = Node("natural")
>>> remote = Node("remote")

We use these nodes to connect the following three elements:

  • Element dam handles the tested dam_v001 model instance.

  • Element stream1 uses one arma_rimorido model instance to route the dam’s outflow with significant delay.

  • Element stream2 uses another arma_rimorido model instance to pass the subcatchment’s additional discharge without delay.

>>> from hydpy import Element
>>> dam = Element("dam", inlets=inflow, outlets=outflow, receivers=remote)
>>> stream1 = Element("stream1", inlets=outflow, outlets=remote)
>>> stream2 = Element("stream2", inlets=natural, outlets=remote)

Next, we prepare the three model instances. We begin with the stream2 model. Setting the Responses parameter in the following manner defines a pure Moving Average model that neither results in translation nor retention:

>>> from hydpy import prepare_model
>>> stream2.model = prepare_model("arma_rimorido")
>>> stream2.model.parameters.control.responses(((), (1.0,)))
>>> stream2.model.parameters.update()

stream2 also works like a pure Moving Average model but causes a time delay of 1.8 days:

>>> stream1.model = prepare_model("arma_rimorido")
>>> stream1.model.parameters.control.responses(((), (0.2, 0.4, 0.3, 0.1)))
>>> stream1.model.parameters.update()

Last but not least, we initialise the dam_v001 instance and hand it to its element (we will define distinct parameter sets for the examples below):

>>> from hydpy.models.dam_v001 import *
>>> parameterstep("1d")
>>> dam.model = model

The IntegrationTest object test serves to execute the following examples conveniently:

>>> from hydpy import IntegrationTest
>>> test = IntegrationTest(dam)
>>> test.inits=((states.watervolume, 0.0),
...             (logs.loggedadjustedevaporation, 0.0),
...             (logs.loggedtotalremotedischarge, 1.9),
...             (logs.loggedoutflow, 0.0),
...             (stream1.model.sequences.logs.login, 0.0))
>>> test.dateformat = "%d.%m."
>>> test.plotting_options.axis1 = fluxes.inflow, fluxes.outflow
>>> test.plotting_options.axis2 = states.watervolume

Next, we create a drought event. The natural discharge of the subcatchment decreases for nine days, stays at a constant level of 1 m³/s for four days, and increases again:

>>> natural.sequences.sim.series = [1.8, 1.7, 1.6, 1.5, 1.4, 1.3, 1.2, 1.1, 1.0, 1.0,
...                                 1.0, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8]

The inflow into the dam remains constant for the whole simulation period:

>>> inflow.sequences.sim.series = 1.0

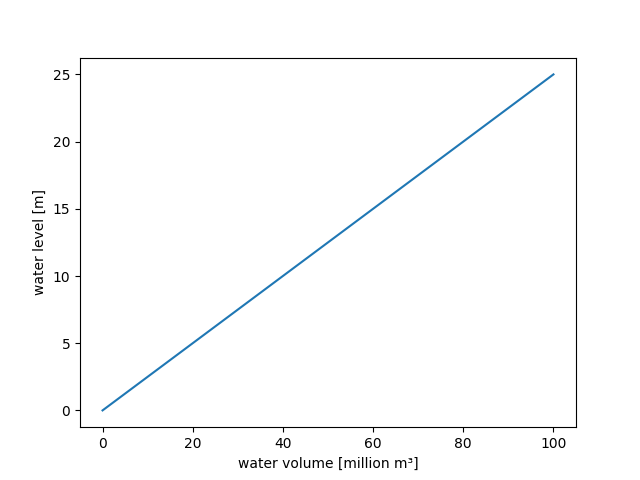
For the sake of simplicity, we define a linear relationship between the stored water volume and the water level. One can accomplish this most easily via method from_data() of class PPoly:

>>> watervolume2waterlevel(PPoly.from_data(xs=[0.0, 1.0], ys=[0.0, 0.25]))

The following figure confirms the linearity of the defined relationship:

>>> figure = watervolume2waterlevel.plot(0.0, 100.0)
>>> from hydpy.core.testtools import save_autofig
>>> save_autofig("dam_v001_watervolume2waterlevel.png", figure=figure)
_images/dam_v001_watervolume2waterlevel.png

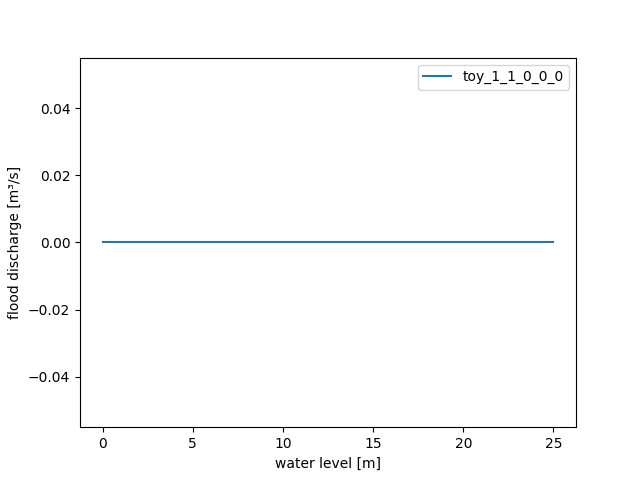
To focus on the drought-related algorithms only, we turn off the flood-related processes. Therefore, we let parameter WaterLevel2FloodDischarge return zero for all possible input values:

>>> waterlevel2flooddischarge(PPoly.from_data(xs=[0.0], ys=[0.0]))
>>> figure = waterlevel2flooddischarge.plot(0.0, 25.0)
>>> save_autofig("dam_v001_waterlevel2flooddischarge_1.png", figure=figure)
_images/dam_v001_waterlevel2flooddischarge_1.png

The exact values of the following parameters are relevant only for those examples where we take precipitation or evaporation into account. Please see the documentation on the simple lake model dam_llake, which discusses these parameters in detail:

>>> surfacearea(1.44)
>>> correctionprecipitation(1.2)
>>> correctionevaporation(1.2)
>>> weightevaporation(0.8)
>>> thresholdevaporation(0.0)
>>> toleranceevaporation(0.001)

We must define the catchment area draining into the dam. dam_v001 requires this information to adjust the numerical local truncation error. For a catchment area of 86.4 km², the general local truncation error (in mm per simulation step) is identical to the applied site-specific local truncation error (in m³/s):

>>> catchmentarea(86.4)
>>> from hydpy import round_
>>> round_(solver.abserrormax.INIT)
0.0001
>>> derived.seconds.update()
>>> solver.abserrormax.update()
>>> solver.abserrormax
abserrormax(0.0001)

If you require higher accuracy or can live with lower accuracy, override this default mechanism by setting any other tolerance value (possible within any control file; see the accuracy drought and the accuracy flood examples for further information).

We enable the RestrictTargetedRelease option flag in the following examples if not stated otherwise:

>>> restricttargetedrelease(True)

no outflow

We temporarily turn off the drought-related functionalities to confirm the proper arrangement of the whole scenario.

>>> nmblogentries(1)
>>> remotedischargeminimum(0.0)
>>> remotedischargesafety(0.0)
>>> neardischargeminimumthreshold(0.0)
>>> neardischargeminimumtolerance(0.0)
>>> waterlevelminimumthreshold(0.0)
>>> waterlevelminimumtolerance(0.0)

The following table confirms that dam_v001 does not release any discharge (the column “outflow” contains zero values only). Hence, the downstream cross-section’s discharge (column “remote”) and the subcatchment’s discharge (column “natural”) are identical:

>>> test("dam_v001_no_outflow")
Click to see the table
Click to see the graph

exact remote minimum

Now, we set the discharge to be not undercut at the cross-section downstream to 1.4 m³/s:

>>> remotedischargeminimum(1.4)

Principally, the dam model attenuates the drought. However, it is not very successful in doing so. In the event’s first half, the cross-section’s lowest discharge increases from 1.0 m³/s to approximately 1.2 m³/s, which is still below the threshold value of 1.4 m³/s. Furthermore, in the event’s second half, dam_v001 works too eagerly, resulting in a discharge of approximately 1.6 m³/s instead of 1.4 m³/s on January 12:

>>> test("dam_v001_exact_remote_minimum")
Click to see the table
Click to see the graph

increased remote minimum

The qualified success in the example above is partly due to the time delay of the information flow from the cross-section to the dam, but the more important factor is the travel time of the released discharge. A simple strategy to increase reliability is to set a higher value for parameter RemoteDischargeMinimum. When defining a value of 1.6 m/s, only minor violations of the actual threshold value remain:

>>> remotedischargeminimum(1.6)
>>> test("dam_v001_increased_remote_minimum")
Click to see the table
Click to see the graph

remote safety

While increasing parameter RemoteDischargeMinimum is always possible, it is often advisable to modify parameter RemoteDischargeSafety instead:

>>> remotedischargeminimum(1.4)
>>> remotedischargesafety(0.5)

For the new configuration, the cross-section’s discharge exceeds the threshold value at each simulation time step. Additionally, the dam’s final storage content is about 4 % higher than in the last example, indicating more efficient water usage:

>>> test("dam_v001_remote_safety")
Click to see the table
Click to see the graph

sharp near minimum

Building upon the last example, we subsequently increase the model’s complexity. Next, we introduce a local minimum water release of 0.2 m³/s:

>>> neardischargeminimumthreshold(0.2)

Consequently, dam_v001 now releases discharge that is not required at the cross-section downstream:

>>> test("dam_v001_sharp_near_minimum")
Click to see the table
Click to see the graph

accuracy drought

One may have noted that the water release is only 0.19 m³/s instead of 0.2 m³/s on January 1. This deviation is due to the low local truncation error of 0.01 m³/s in combination with the simulation starting with a completely dry dam. To confirm this assertion, we increase the required numerical accuracy temporarily:

>>> solver.abserrormax(1e-6)

Now, there is only a tiny deviation left in the last shown decimal place:

>>> test("dam_v001_accuracy_drought")
Click to see the table
Click to see the graph
>>> solver.abserrormax(1e-2)

smooth near minimum

To allow for a smooth transition of the water release in periods where the highest demand switches from “remote” to “near” or the other way around, one can increase the value of the NearDischargeMinimumTolerance parameter:

>>> neardischargeminimumtolerance(0.2)

It is easiest to inspect this “smooth switch” effect by comparing the “required release” column of this and the last example:

>>> test("dam_v001_smooth_near_minimum")
Click to see the table
Click to see the graph

restriction enabled

dam_v001 is forced to keep a certain degree of low flow variability when the option flag RestrictTargetedRelease is enabled. Then, it is not allowed to release an arbitrary amount of water when the inflow falls below the required minimum water release. We show this by decreasing the inflow in the second half of the simulation period to 0.1 m³/s:

>>> inflow.sequences.sim.series[10:] = 0.1

We maintain the value of parameter NearDischargeMinimumThreshold (0.2 m³/s) but change NearDischargeMinimumTolerance to 0 m³/s for better comprehensibility:

>>> neardischargeminimumtolerance(0.0)

As expected, the actual release drops to 0.1 m³/s on January 11. But due to the delay of the discharge released earlier, the strongest violation of the threshold value occurs on January 13:

>>> test("dam_v001_restriction_enabled")
Click to see the table
Click to see the graph

restriction disabled

This modification of the last example shows that with RestrictTargetedRelease being disabled, water release can always exceed the current inflow:

>>> restricttargetedrelease(False)
>>> test("dam_v001_restriction_disabled")
Click to see the table
Click to see the graph
>>> restricttargetedrelease(True)

sharp stage minimum

Another issue relevant to the simulation of drought events is the possible restriction of water release due to limited water availability. To focus on this, we reset the parameter NearDischargeMinimumThreshold to 0 m³/s and define smaller inflow values that constantly decrease from 0.2 m³/s to 0.0 m³/s:

>>> neardischargeminimumthreshold(0.0)
>>> inflow.sequences.sim.series = numpy.linspace(0.2, 0.0, 20)

Now, the storage content increases only until January 5. Afterwards, the dam starts to run dry. On January 11, it is virtually empty, but there are some fluctuations in the water volume around 0 m³. The strongest negative deviation from the “normal empty value” of 0 m³ occurs at the end of January 12, where the storage volume is -666 m³:

>>> test("dam_v001_sharp_stage_minimum")
Click to see the table
Click to see the graph

The fluctuation is due to the discontinuous configuration of the equation underlying method Calc_ActualRelease_V1 around WaterLevelMinimumThreshold and the limited accuracy of the applied numerical integration algorithm. Theoretically, we could decrease AbsErrorMax to reduce this problem significantly. However, this could result in huge computation times, as the implemented Runge-Kutta method is generally incapable of handling discontinuities. Hence, the algorithm would have to substantially decrease the internal calculation time step.

smooth stage minimum

To solve the discussed problem more efficiently than by decreasing AbsErrorMax, we can increase NearDischargeMinimumTolerance, which is a smoothing parameter responsible for smoothing all water level-related discontinuities around WaterLevelMinimumThreshold:

>>> waterlevelminimumtolerance(0.01)

One must also slightly increase WaterLevelMinimumThreshold to avoid the fluctuation and negative water volumes:

>>> waterlevelminimumthreshold(0.005)

Now the dam empties without any fluctuations. The lowest storage content of 541 m³ occurs on January 14. After that date, the dam refills to a certain degree due to the decreasing remote demand. Note that we can circumvent negative water volumes in this example, but this would not happen if the low flow period were prolonged:

>>> test("dam_v001_smooth_stage_minimum")
Click to see the table
Click to see the graph

There is still some inaccuracy in the results. For example, the last outflow value is smaller than AbsErrorMax. However, smoothing the discontinuous relationship would now allow defining a smaller local truncation error without increasing computation times too much.

evaporation

In agreement with the evaporation example of application model dam_llake, we add an evap_ret_io submodel and set the (unadjusted) potential evaporation to 1 mm/d for the first ten days and 5 mm/d for the last ten days:

>>> with model.add_pemodel_v1("evap_ret_io") as pemodel:
...     evapotranspirationfactor(1.0)
>>> pemodel.prepare_inputseries()
>>> pemodel.sequences.inputs.referenceevapotranspiration.series = 10 * [1.0] + 10 * [5.0]

The adjusted evaporation follows the given potential evaporation with a short delay. The increase in evaporation results in a faster decline in the stored water volume. Soon after, actual evaporation drops to zero due to the dam running dry:

>>> test("dam_v001_evaporation")
Click to see the table
Click to see the graph

There are, again, negative water volumes. This time, they are due to smoothing the water level-related threshold ThresholdEvaporation via ToleranceEvaporation. The explanations of the examples sharp stage minimum and smooth stage minimum regarding the functionally similar parameters WaterLevelMinimumThreshold and WaterLevelMinimumTolerance also apply to the case at hand.

>>> del model.pemodel

short memory

The last “drought control” parameter we did not vary so far is NmbLogEntries. In the examples above, its value is always one, meaning that each estimate of the subcatchment’s “natural” discharge is based only on the latest observation. Using only the newest available observation offers the advantage of quick adjustments. But there is a risk of reacting too eagerly, which could result in cyclically fluctuating releases.

We define a series of extreme fluctuations by repeating the natural discharge values of 1.5 m³/s and 0.5 m³/s ten times:

>>> natural.sequences.sim.series = 10 * [1.5, 0.5]

We increase the inflow to 1 m³/s again to ensure the dam can release as much water as it estimates to be required:

>>> inflow.sequences.sim.series = 1.0

Furthermore, we assume no relevant time delay between the dam’s outlet and the cross-section downstream:

>>> stream1.model.parameters.control.responses(((), (1.0,)))
>>> stream1.model.parameters.update()

The example is a little artificial but reveals a general problem that might occur in different forms. Due to the time delay of the information flow from the cross-section to the dam, the dam wastes much water by increasing the high flows without increasing the low flows:

>>> test("dam_v001_short_memory")
Click to see the table
Click to see the graph

long memory

It seems advisable to increase the number of observations for estimating and using a more long-term natural discharge at the cross-section. For this purpose, we set NmbLogEntries to two:

>>> nmblogentries(2)

Now, the water release remains relatively constant. This strategy does not completely solve wasting water during peak flows and violating the low flow threshold, but it significantly reduces these problems:

>>> test("dam_v001_long_memory")
Click to see the table
Click to see the graph

We cannot circumvent the general problem of a time delay of one simulation step for the information flow from the cross-section to the dam. To solve it, we would have to simultaneouslyh andle the differential equations of all models involved, which is currently not supported by HydPy and is impossible for most implemented models. However, due to the low dynamics of drought events, the resulting inaccuracies should rarely be substantial.

flood retention

This example and the following ones demonstrate the proper implementation of the flood retention functionalities. For simplicity, we deactivate all parameters related to low water calculations:

>>> nmblogentries(1)
>>> remotedischargeminimum(0.0)
>>> remotedischargesafety(0.0)
>>> neardischargeminimumthreshold(0.0)
>>> neardischargeminimumtolerance(0.0)
>>> waterlevelminimumthreshold(0.0)
>>> waterlevelminimumtolerance(0.0)

We define a linear storage retention process to compare the following numerical results of dam_v001 with an analytical solution. The relationship between water volume and level is already linear, and we adjust the relationship between water level and flood discharge accordingly:

>>> waterlevel2flooddischarge(PPoly.from_data(xs=[0.0, 1.0], ys= [0.0, 2.5]))
>>> figure = waterlevel2flooddischarge.plot(0.0, 25.0)
>>> save_autofig("dam_v001_waterlevel2flooddischarge_2.png", figure=figure)
_images/dam_v001_waterlevel2flooddischarge_2.png

The linear storage coefficient for the given simulation step size is approximately 0.054/d.

Now, we add a meteo_precip_io submodel and define a precipitation series including only a heavy one-day rainfall event and a corresponding inflowing flood wave, starting and ending with zero discharge:

>>> with model.add_precipmodel_v2("meteo_precip_io") as precipmodel:
...     precipitationfactor(1.0)
>>> precipmodel.prepare_inputseries()
>>> precipmodel.sequences.inputs.precipitation.series = [
...     0.0, 50.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
...     0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
>>> inflow.sequences.sim.series = [0.0, 0.0, 5.0, 9.0, 8.0, 5.0, 3.0, 2.0, 1.0, 0.0,
...                                0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

For the sake of simplicity, we assume a constant “natural” discharge of 1 m³/s of the subcatchment:

>>> test.inits.loggedtotalremotedischarge = 1.0
>>> natural.sequences.sim.series = 1.0

In this example, we use the default accuracy of 0.01 m³/s, which should be sufficient for most flood simulations for large dams:

>>> solver.abserrormax
abserrormax(0.01)

When discussing the simulation of flood events, we should examine numerical stability and accuracy and their relation to computation time more closely. We use the number of calls of the differential equations as an indicator for computation time. To do so, we first set the corresponding counter to zero:

>>> model.numvars.nmb_calls = 0

The following graph shows that dam_v001 works like the linear storage approach under the given configuration:

>>> test("dam_v001_flood_retention")
Click to see the table
Click to see the graph

For a more precise evaluation, you can compare the dam’s outflow with the following results of the linear storage cascade with a single bucket:

>>> from hydpy.auxs.iuhtools import LinearStorageCascade
>>> lsc = LinearStorageCascade(n=1, k=1.0/0.054)
>>> inflow = fluxes.adjustedprecipitation.series + inflow.sequences.sim.series
>>> outflow = numpy.convolve(lsc.ma.coefs, inflow)
>>> from hydpy import print_vector
>>> print_vector(outflow[:20])
0.0, 0.02652, 0.183776, 0.543037, 0.961081, 1.251541, 1.395548,
1.453371, 1.455585, 1.405116, 1.331252, 1.261271, 1.194968, 1.132151,
1.072636, 1.01625, 0.962828, 0.912214, 0.864261, 0.818829

The largest difference occurs on January 1. But this difference of 0.000054 m³/s is way below the required accuracy of 0.01 m³/s. There is no guarantee that the actual numerical error will always fall below the defined tolerance value, but if everything works well, we have good reason to hope this happens in many cases. At least for sufficiently smooth problems, the actual error should be better than the error estimate by one order. However, one can never rule out the risk of error accumulations over multiple simulation steps.

dam_v001 required about four calls per simulation step on average:

>>> model.numvars.nmb_calls
78
>>> model.numvars.nmb_calls = 0

accuracy flood

If we set the tolerance value to 1e-6 m³/s, the six decimal places in the following table show no deviation from the analytical solution of the linear storage equation:

>>> solver.abserrormax(1e-6)
>>> test("dam_v001_accuracy_flood")
Click to see the table
Click to see the graph

This improvement in accuracy comes with a significant increase in computation time. dam_v001 required 10.5 calls on average:

>>> model.numvars.nmb_calls
211
>>> model.numvars.nmb_calls = 0

stiffness

We reset the local error tolerance to the more practical value but configure the WaterLevel2FloodDischarge parameter in a highly dynamic manner:

>>> solver.abserrormax(0.01)
>>> waterlevel2flooddischarge(PPoly.from_data(xs=[0.0, 1.0], ys=[0.0, 250.0]))
>>> figure = waterlevel2flooddischarge.plot(0.0, 25.0)
>>> save_autofig("dam_v001_waterlevel2flooddischarge_3.png", figure=figure)
_images/dam_v001_waterlevel2flooddischarge_3.png

Due to the high linear storage coefficient of approximately 5.4 per day, the following test results show virtually no retention effects:

>>> test("dam_v001_stiffness")
Click to see the table
Click to see the graph

The following comparative calculation shows that dam_v001 reaches the desired numerical accuracy for this extreme parameterisation:

>>> lsc.k = 1.0/5.4
>>> print_vector(numpy.convolve(lsc.ma.coefs, inflow)[:20])
0.0, 0.815651, 4.261772, 8.259271, 8.181003, 5.553864, 3.371199,
2.186025, 1.185189, 0.185185, 0.000836, 0.000004, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0

However, stability issues required dividing the simulation steps into shorter internal substeps, which increased the average number of calls per simulation step to 19.

>>> model.numvars.nmb_calls
358
>>> model.numvars.nmb_calls = 0

Also, note that the final water volume is negative due to the limited numerical accuracy of the results.

This stability issue should seldom be relevant for typical simulations of dam retention processes. But one should keep it in mind when playing around with parameters, for example, during model calibration. Otherwise, unexpectedly long simulation durations might occur.

class hydpy.models.dam_v001.Model[source]

Bases: Main_PrecipModel_V2, Main_PEModel_V1

HydPy-Dam-V1 (dam model, version 1).

The following “receiver update methods” are called in the given sequence before performing a simulation step:
The following “inlet update methods” are called in the given sequence at the beginning of each simulation step:
The following methods define the relevant components of a system of ODE equations (e.g. direct runoff):
The following methods define the complete equations of an ODE system (e.g. change in storage of fast water due to effective precipitation and direct runoff):
The following “outlet update methods” are called in the given sequence at the end of each simulation step:

  • Calc_WaterLevel_V1 Determine the water level based on an interpolation approach approximating the relationship between water volume and water level.

  • Pass_Outflow_V1 Update the outlet link sequence Q.

  • Update_LoggedOutflow_V1 Log a new entry of discharge at a cross section far downstream.

Users can hook submodels into the defined main model if they satisfy one of the following interfaces:

  • PrecipModel_V2 Simple interface for determining precipitation in one step.

  • PETModel_V1 Simple interface for calculating all potential evapotranspiration values in one step.

DOCNAME: DocName = ('Dam-V1', 'dam model, version 1')
precipmodel: modeltools.SubmodelProperty

Optional submodel that complies with the following interface: PrecipModel_V2.

pemodel: modeltools.SubmodelProperty

Optional submodel that complies with the following interface: PETModel_V1.

REUSABLE_METHODS: ClassVar[tuple[type[ReusableMethod], ...]] = ()
class hydpy.models.dam_v001.ControlParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Control parameters of model dam_v001.

The following classes are selected:
class hydpy.models.dam_v001.DerivedParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Derived parameters of model dam_v001.

The following classes are selected:
class hydpy.models.dam_v001.FactorSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: FactorSequences

Factor sequences of model dam_v001.

The following classes are selected:
class hydpy.models.dam_v001.FluxSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: FluxSequences

Flux sequences of model dam_v001.

The following classes are selected:
class hydpy.models.dam_v001.InletSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: InletSequences

Inlet sequences of model dam_v001.

The following classes are selected:

  • Q() Inflow [m³/s].

class hydpy.models.dam_v001.LogSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: LogSequences

Log sequences of model dam_v001.

The following classes are selected:
class hydpy.models.dam_v001.OutletSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: OutletSequences

Outlet sequences of model dam_v001.

The following classes are selected:

  • Q() Outflow [m³/s].

class hydpy.models.dam_v001.ReceiverSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: ReceiverSequences

Receiver sequences of model dam_v001.

The following classes are selected:

  • Q() Remote discharge [m³/s].

class hydpy.models.dam_v001.SolverParameters(master: Parameters, cls_fastaccess: type[FastAccessParameter] | None = None, cymodel: CyModelProtocol | None = None)

Bases: SubParameters

Solver parameters of model dam_v001.

The following classes are selected:

  • AbsErrorMax() Absolute numerical error tolerance [m³/s].

  • RelErrorMax() Relative numerical error tolerance [1/T].

  • RelDTMin() Smallest relative integration time step size allowed [-].

  • RelDTMax() Largest relative integration time step size allowed [-].

class hydpy.models.dam_v001.StateSequences(master: Sequences, cls_fastaccess: type[TypeFastAccess_co] | None = None, cymodel: CyModelProtocol | None = None)

Bases: StateSequences

State sequences of model dam_v001.

The following classes are selected: